SPSS二元Logistic回归结果分析.docx
《SPSS二元Logistic回归结果分析.docx》由会员分享,可在线阅读,更多相关《SPSS二元Logistic回归结果分析.docx(13页珍藏版)》请在冰点文库上搜索。
SPSS二元Logistic回归结果分析
SPSS—二元Logistic回归结果分析
2011-12-0216:
48
身心疲惫,睡意连连,头不断往下掉,拿出耳机,听下歌曲,缓解我这严重的睡意吧!
今天来分析二元Logistic回归的结果
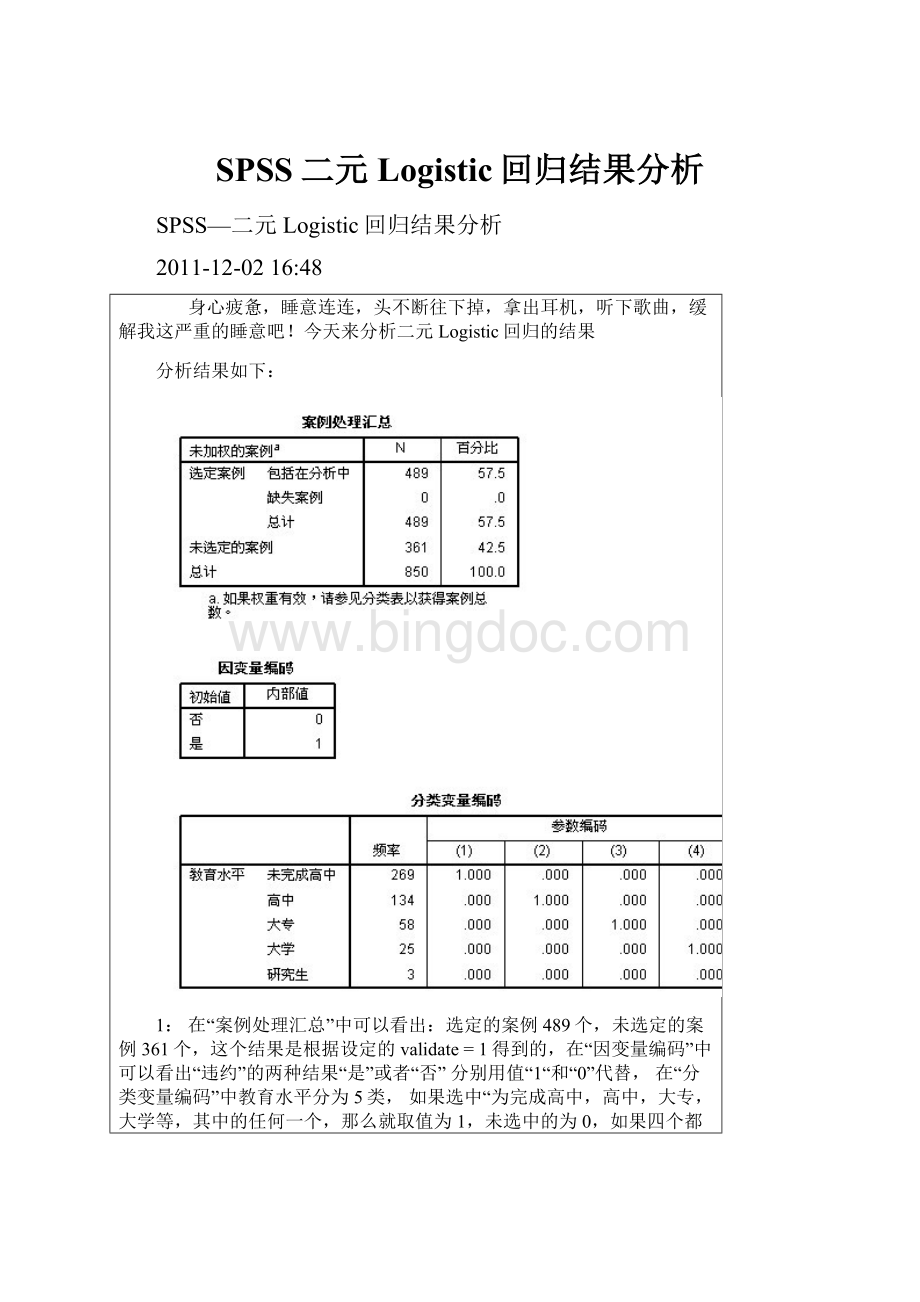
分析结果如下:
1:
在“案例处理汇总”中可以看出:
选定的案例489个,未选定的案例361个,这个结果是根据设定的validate=1得到的,在“因变量编码”中可以看出“违约”的两种结果“是”或者“否”分别用值“1“和“0”代替,在“分类变量编码”中教育水平分为5类,如果选中“为完成高中,高中,大专,大学等,其中的任何一个,那么就取值为1,未选中的为0,如果四个都未被选中,那么就是”研究生“频率分别代表了处在某个教育水平的个数,总和应该为489个
1:
在“分类表”中可以看出:
预测有360个是“否”(未违约)有129个是“是”(违约)
2:
在“方程中的变量”表中可以看出:
最初是对“常数项”记性赋值,B为,标准误差为:
那么wald=(B/²=²=,跟表中的“几乎接近,是因为我对数据进行的向下舍入的关系,所以数据会稍微偏小,
B和Exp(B)是对数关系,将B进行对数抓换后,可以得到:
Exp(B)=e^=, 其中自由度为1,sig为,非常显著
1:
从“不在方程中的变量”可以看出,最初模型,只有“常数项”被纳入了模型,其它变量都不在最初模型内
表中分别给出了,得分,df, Sig三个值, 而其中得分(Score)计算公式如下:
(公式中(Xi-X¯)少了一个平方)
下面来举例说明这个计算过程:
(“年龄”自变量的得分为例)
从“分类表”中可以看出:
有129人违约,违约记为“1” 则违约总和为129,选定案例总和为489
那么:
y¯=129/489=
x¯=16951/489=
所以:
∑(Xi-x¯)²=
y¯(1-y¯)= *()=
则:
y¯(1-y¯)* ∑(Xi-x¯)²=*=5
则:
[∑Xi(yi-y¯)]^2=
所以:
=/5==(四舍五入)
计算过程采用的是在EXCEL里面计算出来的,截图如下所示:
从“不在方程的变量中”可以看出,年龄的“得分”为,刚好跟计算结果吻合!
!
答案得到验证~!
!
!
!
1:
从“块1”中可以看出:
采用的是:
向前步进的方法,在“模型系数的综合检验”表中可以看出:
所有的SIG几乎都为“0” 而且随着模型的逐渐步进,卡方值越来越大,说明模型越来越显著,在第4步后,终止,
根据设定的显著性值和 自由度,可以算出卡方临界值,公式为:
=CHIINV(显著性值,自由度) ,放入excel就可以得到结果
2:
在“模型汇总“中可以看出:
Cox&SnellR方 和NagelkerkeR方拟合效果都不太理想,最终理想模型也才:
和,
最大似然平方的对数值都比较大,明显是显著的
似然数对数计算公式为:
计算过程太费时间了,我就不举例说明计算过程了
Cox&SnellR方的计算值 是根据:
1:
先拟合不包含待检验因素的Logistic模型,求对数似然函数值INL0 (指只包含“常数项”的检验)
2:
再拟合包含待检验因素的Logistic模型,求新的对数似然函数值InLB (包含自变量的检验)
再根据公式:
即可算出:
Cox&SnellR方的值!
提示:
将Hosmer和Lemeshow检验和“随机性表”结合一起来分析
1:
从 Hosmer和Lemeshow检验表中,可以看出:
经过4次迭代后,最终的卡方统计量为:
,而临界值为:
CHINV,8)=
卡方统计量<临界值,从SIG角度来看:
>,说明模型能够很好的拟合整体,不存在显著的差异。
2:
从Hosmer和Lemeshow检验随即表中可以看出:
”观测值“和”期望值“几乎是接近的,不存在很大差异,说明模型拟合效果比较理想,印证了“Hosmer和Lemeshow检验”中的结果
而“Hosmer和Lemeshow检验”表中的“卡方”统计量,是通过“Hosmer和Lemeshow检验随即表”中的数据得到的(即通过“观测值和”预测值“)得到的,计算公式如下所示:
x²(卡方统计量)= ∑(观测值频率-预测值频率)^2/预测值的频率
举例说明一下计算过程:
以计算"步骤1的卡方统计量为例"
1:
将“Hosmer和Lemeshow检验随即表”中“步骤1” 的数据,复制到excel中,得到如下所示结果:
从“Hosmer和Lemeshow检验”表中可以看出,步骤1的卡方统计量为:
, 在上图中,通过excel计算得到,结果为 ~~(四舍五入),结果是一致的,答案得到验证!
!
1:
从“分类表”—“步骤1”中可以看出:
选定的案例中,“是否曾今违约”总计:
489个,其中没有违约的360个,并且对360个“没有违约”的客户进行了预测,有340个预测成功,20个预测失败,预测成功率为:
340/360=%
其中“违约”的有189个,也对189个“违约”的客户进行了预测,有95个预测失败,34个预测成功,预测成功率:
34/129=%
总计预测成功率:
(340+34)/489=%
步骤1的总体预测成功率为:
%,在步骤4终止后,总体预测成功率为:
,预测准确率逐渐提升%—%—%—。
的预测准确率,不能够算太高,只能够说还行。
从“如果移去项则建模”表中可以看出:
“在-2对数似然中的更改”中的数值是不是很眼熟,跟在“模型系数总和检验”表中“卡方统计量"量的值是一样的!
!
!
将“如果移去项则建模”和“方程中的变量”两个表结合一起来看
1:
在“方程中的变量”表中可以看出:
在步骤1中输入的变量为“负债率” ,在”如果移去项则建模“表中可以看出,当移去“负债率”这个变量时,引起了的数值更改,此时模型中只剩下“常数项”为常数项的对数似然值
在步骤2中,当移去“工龄”这个自变量时,引起了的数值变化(简称:
似然比统计量),在步骤2中,移去“工龄”这个自变量后,还剩下“负债率”和“常量”,此时对数似然值变成了:
,此时我们可以通过公式算出“负债率”的似然比统计量:
计算过程如下:
似然比统计量=2(+)= 答案得到验证!
!
!
2:
在“如果移去项则建模”表中可以看出:
不管移去那一个自变量,“更改的显著性”都非常小,几乎都小于,所以这些自变量系数跟模型显著相关,不能够剔去!
!
3:
根据"方程中的变量“这个表,我们可以得出logistic回归模型表达式:
= 1/1+e^-(a+∑βI*Xi) 我们假设Z=
那么可以得到简洁表达式:
P(Y)=1/1+e^(-z)
将”方程中的变量“—步骤4中的参数代入 模型表达式中,可以得到 logistic回归模型如下所示:
P(Y)=1/1+e^-(+*信用卡负债率+*负债率*地址*功龄)
从”不在方程中的变量“表中可以看出:
年龄,教育,收入,其它负债,都没有纳入模型中,其中:
sig值都大于,所以说明这些自变量跟模型显著不相关。
在”观察到的组和预测概率图”中可以看出:
1:
theCutValueis, 此处以为切割值,预测概率大于,表示客户“违约”的概率比较大,小于表示客户“违约”概率比较小。
2:
从上图中可以看出:
预测分布的数值基本分布在“左右两端”在大于的切割值中,大部分都是“1”表示大部分都是“违约”客户,(大约230个违约客户)预测概率比较准,而在小于的切割值中,大部分都是“0”大部分都是“未违约”的客户,(大约500多个客户,未违约)预测也很准
在运行结束后,会自动生成多个自变量,如下所示:
1:
从上图中可以看出,已经对客户“是否违约”做出了预测,上面用颜色标记的部分-PRE_1表示预测概率,
上面的预测概率,可以通过前面的Logistic回归模型计算出来,计算过程不演示了
2:
COOK_1 和SRE_1的值可以跟预测概率(PRE_1)进行画图,来看COOK_1和SRE_1对预测概率的影响程度,因为COOK值跟模型拟合度有一定的关联,发生奇异值,会影响分析结果。
如果有太多奇异值,应该单独进行深入研究!