初三中考数学动点型题复习文档格式.doc

初三中考数学动点型题复习文档格式.doc

《初三中考数学动点型题复习文档格式.doc》由会员分享，可在线阅读，更多相关《初三中考数学动点型题复习文档格式.doc（21页珍藏版）》请在冰点文库上搜索。

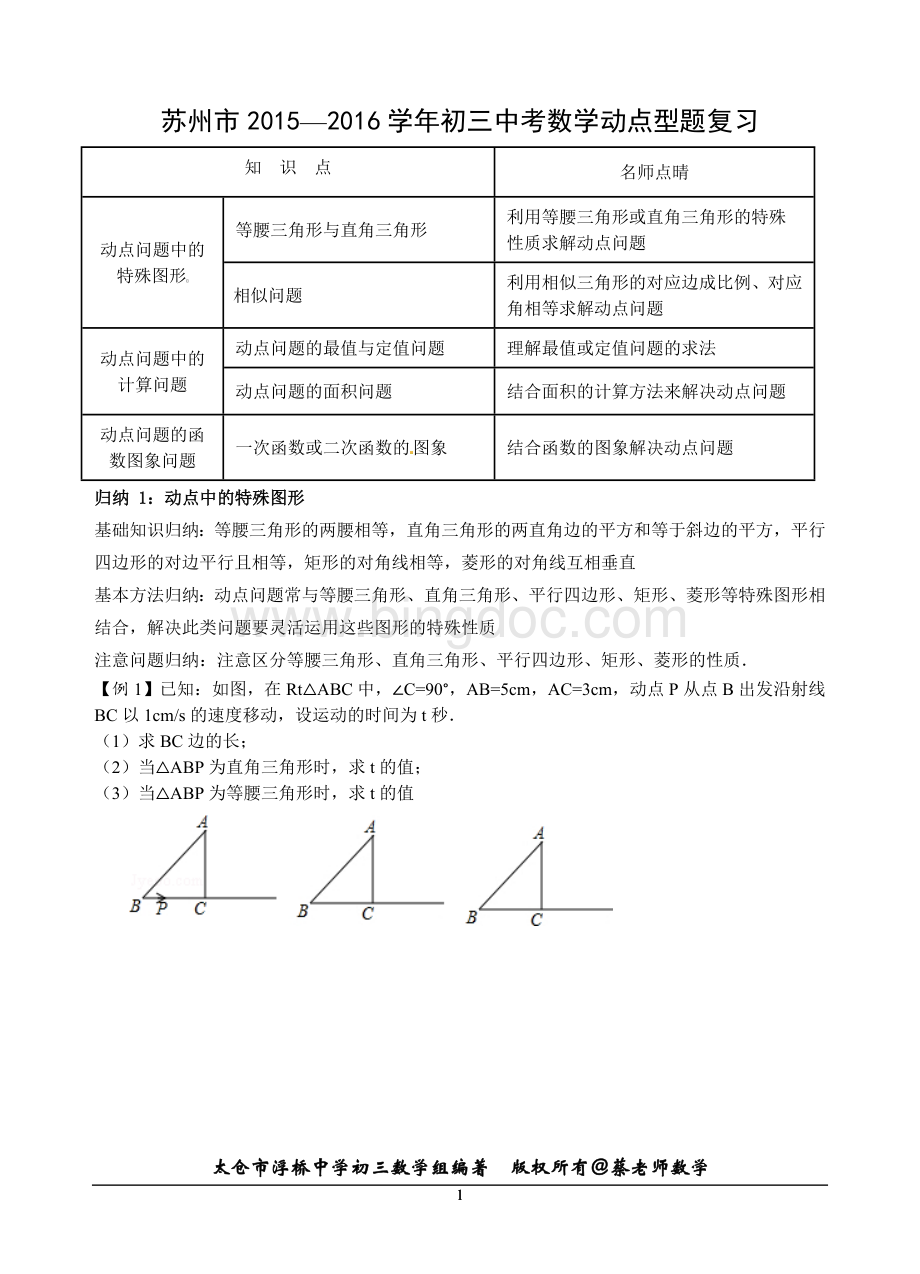
（例2图）

练习：

（2013•日照）问题背景：

如图（a），点A、B在直线l的同侧，要在直线l上找一点C，使AC与BC的距离之和最小，我们可以作出点B关于l的对称点B′，连接AB′与直线l交于点C，则点C即为所求．

（1）实践运用：

如图（b），已知，⊙O的直径CD为4，点A在⊙O上，∠ACD=30°

，B为弧AD的中点，P为直径CD上一动点，则BP+AP的最小值为　　．

（2）知识拓展：

如图（c），在Rt△ABC中，AB=10，∠BAC=45°

，∠BAC的平分线交BC于点D，E、F分别是线段AD和AB上的动点，求BE+EF的最小值，并写出解答过程．

归纳3：

动点问题的图象

动点问题经常与一次函数、反比例函数和二次函数的图象相结合．

一次函数图象是一条直线，反比例函数图象是双曲线，二次函数图象是抛物线．

动点函数的图象问题可以借助于相似、特殊图形的性质求出函数的图象解析式，同时也可以观察图象的变化趋势．

【例3】如图，在矩形ABCD中，AB=2，点E在边AD上，∠ABE=45°

，BE=DE，连接BD，点P在线段DE上，过点P作PQ∥BD交BE于点Q，连接QD．设PD=x，△PQD的面积为y，则能表示y与x函数关系的图象大致是（　　）

归纳4：

函数中的动点问题

函数中的动点问题的背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；

分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：

等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

一是利用动点（图形）位置进行分类，把运动问题分割成几个静态问题，然后运用转化的思想和方法将几何问题转化为函数和方程问题；

二是利用函数与方程的思想和方法将所解决图形的性质（或所求图形面积）直接转化为函数或方程。

化动为静，画出符合条件的图形。

【例4】

（2015年江苏盐城12分）如图，在平面直角坐标系xOy中，将抛物线的对称轴绕着点P（，2）顺时针旋转45°

后与该抛物线交于A、B两点，点Q是该抛物线上的一点.

（1）求直线AB的函数表达式；

（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；

（3）如图②，若点Q在y轴左侧，且点T（0，t）（t<

2）是直线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值.

巩固练习：

1.（2015年江苏扬州3分）如图，已知Rt△ABC中，∠ABC=90°

，AC=6，BC=4，将△ABC绕直角顶点C顺时针旋转90°

得到△DEC，若点F是DE的中点，连接AF，则AF=▲．

2.（2015年江苏宿迁3分）如图，在平面直角坐标系中，点P的坐标为（0，4），直线与x轴、y轴分别交于点A，B，点M是直线AB上的一个动点，则PM长的最小值为▲．

（第1题）（第2题）

3.（2015年江苏连云港12分）在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．

（1）小明发现DG⊥BE，请你帮他说明理由．

（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．

（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，将线段DG与线段BE相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．

4.如图①，正方形的顶点的坐标分别为，顶点在第一象限．点从点出发，沿正方形按逆时针方向匀速运动，同时，点从点出发，沿轴正方向以相同速度运动．当点到达点时，两点同时停止运动，设运动的时间为秒．

（1）求正方形的边长．

（2）当点在边上运动时，的面积（平方单位）与时间（秒）之间的函数图象为抛物线的一部分（如图②所示），求两点的运动速度．

（3）求

（2）中面积（平方单位）与时间（秒）的函数关系式及面积取最大值时点坐标．

图①

图②

（4）若点保持

（2）中的速度不变，则点沿着边运动时，的大小随着时间的增大而增大；

沿着边运动时，的大小随着时间的增大而减小．当点沿着这两边运动时，使的点有　　　　　个．

中午作业：

1．（2014年甘肃天水）如图，扇形OAB动点P从点A出发，沿线段BO、OA匀速运动到点A，则OP的长度y与运动时间t之间的函数图象大致是（）

A．B．C．D．

2．（2014年贵州安顺）如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°

，点B为劣弧AN的中点．点P是直径MN上一动点，则PA+PB的最小值为（）

A．B．C．D．

（第2题）（第4题）（第5题）

3．如图，矩形ABCD中，AB=3，BC=4，动点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数图象大致是（）

A.B．C．D．

4．（2014年江苏苏州）如图，直线l与半径为4的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l，垂足为B，连接PA．设PA＝x，PB＝y，则（x－y）的最大值是．

5．（2014年四川资阳）如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，点Q为对角线AC上的动点，则△BEQ周长的最小值为__________

6．（2014年浙江嘉兴中考）如图，点C在以AB为直径的半圆上，AB=8，∠CBA=30°

，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F．下列结论：

①CE=CF；

②线段EF的最小值为；

③当AD=2时，EF与半圆相切；

④若点F恰好落在BC上，则AD=；

⑤当点D从点A运动到点B时，线段EF扫过的面积是．其中正确结论的序号是．

（第6题）

7.（2015柳州）如图，在四边形ABCD中，AD∥BC，∠B=90°

，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C运动，点P从点A出发的同时点Q从点C出发，以1cm/s速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动时间为t秒．

（1）从运动开始，当t取何值时，PQ∥CD？

（2）从运动开始，当t取何值时，△PQC为直角三角形？

8.（2015年江苏苏州10分）如图，在矩形ABCD中，AD=acm，AB=bcm（a＞b＞4），半径为2cm的⊙O在矩形内且与AB、AD均相切．现有动点P从A点出发，在矩形边上沿着A→B→C→D的方向匀速移动，当点P到达D点时停止移动；

⊙O在矩形内部沿AD向右匀速平移，移动到与CD相切时立即沿原路按原速返回，当⊙O回到出发时的位置（即再次与AB相切）时停止移动．已知点P与⊙O同时开始移动，同时停止移动（即同时到达各自的终止位置）．

（1）如图①，点P从A→B→C→D，全程共移动了▲cm（用含a、b的代数式表示）；

（2）如图①，已知点P从A点出发，移动2s到达B点，继续移动3s，到达BC的中点．若点P与⊙O的移动速度相等，求在这5s时间内圆心O移动的距离；

（3）★★如图②，已知a=20，b=10．是否存在如下情形：

当⊙O到达⊙O1的位置时（此时圆心O1在矩形对角线BD上），DP与⊙O1恰好相切？

请说明理由．

回家作业：

1.（2015盐城）如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致是（　　）

A．B．C．D．

2.（2015乐山）如图，已知直线与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB．则△PAB面积的最大值是（　　）

A．8B．12C．D．

（第2题）（第3题）

3.（2015咸宁）如图，已知正方形ABCD的边长为2，E是边BC上的动点，BF⊥AE交CD于点F，垂足为G，连结CG．下列说法：

①AG＞GE；

②AE=BF；

③点G运动的路径长为π；

④CG的最小值为．其中正确的说法是．（把你认为正确的说法的序号都填上）

4.（2015年江苏徐州8分）如图，在矩形OABC中，OA=3，OC=5,分别以OA、OC所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数的图像经过点D且与边BA交于点E，连接DE.

（1）连接OE，若△EOA的面积为2，则k=；

（2）连接CA、DE与CA是否平行？

请说明理由；

（3）是否存在点D，使得点B关于DE的对称点在OC上？

若存在，求出点D的坐标；

若不存在，请说明理由.

5.（2015年江苏宿迁8分）如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．

（1）求k的值；

（2）求△BMN面积的最大值；

（3）若MA⊥AB，求t的值．

6.（2015年江苏常州10分）如图，一次函数的图象与x轴、y轴分别相交于点A、B，过点A作x轴的垂线l，点P为直线l上的动点，点Q为直线AB与△OAP外接圆的交点，点P、Q与点A都不重合．

（1）写出点A的坐标；

（2）当点P在直线l上运动时，是否存在点P使得△OQB与△APQ全等？

如果存在，求出点P的坐标；

如果不存在，请说明理由．

（3）若点M在直线l上，且∠POM=90°

，记△OAP外接圆和△OAM外接圆的面积分别是S1、S2，求的值．

参考答案

例1.解：

（1）在Rt△ABC中，BC2=AB2﹣AC2=52﹣32=16，∴BC=4（cm）；

（2）由题意知BP=tcm，①当∠APB为直角时，点P与点C重合，BP=BC=4cm，即t=4；

②当∠BAP为直角时，BP=tcm，CP=（t﹣4）cm，AC=3cm，在Rt△ACP中，

AP2=32+（t﹣4）2，在Rt△BAP中，AB2+AP2=BP2，即：

52+[32+（t﹣4）2]=t2，解得：

t=，

故当△ABP为直角三角形时，t=4或t=；

（3）①当AB=BP时，t=5；

②当AB=AP时，BP=2BC=8cm，t=8；

③当BP=AP时，AP=BP=tcm，CP=|t﹣4|cm，AC=3cm，在Rt△ACP中，AP2=AC2+CP2，

所以t2=32+（t﹣4）2，解得：

综上所述：

当△ABP为等腰三角形时，t=5或t=8或t=．

【点评】本题考查了勾股定理以及等腰三角形的知识，解答本题的关键是掌握勾股定理的应用，以及分情况讨论，注意不要漏解．

例2.【答案】C．【解析】解：

如图，过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，

∵AD是∠BAC的平分线．∴PQ=PM，这时PC+PQ有最小值，即CM的长度，

∵AC=6，BC=8，∠ACB=90°

，∴AB=，

∵S△ABC=AB•CM=AC•BC，∴CM==．

考点：

1.轴对称的应用（最短路线问题）；

2．角平分线的性质；

3．勾股定理；

4．直角三角形的面积．

解：

（1）作点B关于CD的对称点E，连接AE交CD于点P，此时PA+PB最小，且等于AE．作直径AC′，连接C′E．根据垂径定理得=．∵∠ACD=30°

，∴∠AOD=60°

，∠DOE=30°

，

∴∠AOE=90°

，∴∠C′AE=45°

，又AC′为圆的直径，∴∠AEC′=90°

，∴∠C′=∠C′AE=45°

∴C′E=AE=AC′=2，即AP+BP的最小值是2．故答案为：

2；

（2）如图，在斜边AC上截取AB′=AB，连结BB′．∵AD平分∠BAC，∴∠B′AM=∠BAM，

在△B′AM和△BAM中，，∴△B′AM≌△BAM（SAS），

∴BM=B′M，∠BMA=∠B′MA=90°

，∴点B与点B′关于直线AD对称．过点B′作B′F⊥AB，垂足为F，交AD于E，连结BE，则线段B′F的长即为所求．（点到直线的距离最短）在Rt△AFB′中，∵∠BAC=45°

，AB′=AB=10，∴B′F=AB′•sin45°

=AB•sin45°

=10×

=5，

∴BE+EF的最小值为．

例3.【答案】C．【解析】

∵∠ABE=45°

，∠A=90°

，∴△ABE是等腰直角三角形，∴AE=AB=2，BE=AB=2，

∵BE=DE，PD=x，∴PE=DE﹣PD=2﹣x，∵PQ∥BD，BE=DE，∴QE=PE=2﹣x，

又∵△ABE是等腰直角三角形（已证），∴点Q到AD的距离=（2﹣x）=2﹣x,

∴△PQD的面积y=x（2﹣x）=﹣（x2﹣2x+2）=﹣（x﹣）2+,

即y=﹣（x﹣）2+，纵观各选项，只有C选项符合．

动点问题的函数图象．

例4.解：

（1）如答图1，设直线AB与轴的交点为M，

∵，P（，2），∴.

设直线AB的解析式为，

则，解得.∴直线AB的解析式为.

（2）如答图2，过点Q作轴的垂线QC，交AB于点C，再过点Q作直线AB的垂线，垂足为点D，根据条件可知，是等腰直角三角形.

∴.

设，则，

∴当时，点Q到直线AB的距离的最大值为.

（3）∵，∴中必有一角等于45°

.

①由图可知，不合题意.

②若，

如答图3，过点B作轴的平行线与轴和抛物线

分别交于点，此时，.

根据抛物线的轴对称性质，知，

∴是等腰直角三角形.

∵与相似，且，

∴也是等腰直角三角形.

i）若，

联立，解得或.

∴.∴.∴，此时，.

ii）若，，此时，.

③若，②是情况之一，答案同上.

如答图4，5，过点B作轴的平行线与轴和抛物线分别交于点，以点为圆心，为半径画圆，则都在上，设与y轴左侧的抛物线交于另一点.

∵根据圆周角定理，，

∴点也符合要求.

设，

由得解得或，

而，故.∴.

可证是等边三角形，∴.

则在中，.

如答图4，过点作轴于点，

则，

∴，此时，.

ii）若，

如答图5，过点作轴于点，

设，则.

∵，∴，.∴.

综上所述，所有满足条件的t的值为或或或.

1.如答图，连接，过点作于点，

∵在Rt△ABC中，∠ABC=90°

，点F是DE的中点，

∴.∴是等腰三角形.

∵将△ABC绕直角顶点C顺时针旋转90°

得到△DEC，BC=4，AC=6，∴.

∵，∴.∴

又∵分别是的中点，∴是△DEC的中位线.∴.

在Rt△AGF中，∵，，∴由勾股定理，得AF=5.

2.根据垂线段最短得出PM⊥AB时线段PM最短，分别求出PB、OB、OA、AB的长度，利用△PBM∽△ABO，即可求出答案

如答图，过点P作PM⊥AB，则：

∠PMB=90°

当PM⊥AB时，PM最短，

∵直线与x轴、y轴分别交于点A，B，

∴点A的坐标为（4，0），点B的坐标为（0，﹣3）.

在Rt△AOB中，∵AO=4，BO=3，∴根据勾股定理，得AB=5.

∵∠BMP=∠AOB=90°

，∠ABO=∠PBM，

∴△PBM∽△ABO.∴，即：

，解得.

3.解：

（1）∵四边形ABCD和四边形AEFG都为正方形，∴AD=AB，∠DAG=∠BAE=90°

，AG=AE，

∴△ADG≌△ABE（SAS）.∴∠AGD=∠AEB.

如答图1，延长EB交DG于点H，

在△ADG中，∵∠AGD+∠ADG=90°

∴∠AEB+∠ADG=90°

在△EDH中，∵∠AEB+∠ADG+∠DHE=180°

∴∠DHE=90°

.∴DG⊥BE.

（2）∵四边形ABCD和四边形AEFG都为正方形，∴AD=AB，∠DAB=∠GAE=90°

∴∠DAB+∠BAG=∠GAE+∠BAG，即∠DAG=∠BAE，∴△ADG≌△ABE（SAS）.∴DG=BE.

如答图2，过点A作AM⊥DG交DG于点M，则∠AMD=∠AMG=90°

∵BD为正方形ABCD的对角线，∴∠MDA=45°

.在Rt△AMD中，∵∠MDA=45°

，AD=2，

∴.在Rt△AMG中，根据勾股定理得：

∵，∴.

（3）△GHE和△BHD面积之和的最大值为6，理由如下：

∵对于△EGH，点H在以EG为直径的圆上，∴当点H与点A重合时，△EGH的高最大；

∵对于△BDH，点H在以BD为直径的圆上，∴当点H与点A重合时，△BDH的高最大.

∴△GHE和△BHD面积之和的最大值为2+4=6．

【考点】面动旋转问题；

正方形的性质；

全等三角形的判定和性质；

三角形内角和定理；

等腰直角三角形的性质，勾股定理；

数形结合思想的应用．

4.[解]

（1）作轴于．，．．

（2）由图②可知，点从点运动到点用了10秒．又．

两点的运动速度均为每秒1个单位．

（3）方法一：

作轴于，则．，即．．

．，．

即．，且，

当时，有最大值．此时，

点的坐标为．

方法二：

当时，．

设所求函数关系式为．抛物线过点，

．

，且，当时，有最大值．

此时，点的坐标为．

（4）．

[点评]本题主要考查函数性质的简单运用和几何知识，是近年来较为流行的试题，解题的关键在于结合题目的要求动中取静，相信解决这种问题不会非常难

1.【答案】D．考点：

1．动点问题的函数图象；

2．分类思想的应用．

2.【答案】A．考点：

1．轴对称的应用（最短路线问题）；

2．圆周角定理；

3．等腰直角三角形的判定和性质．

（2题答图）（3题答图）（4题答图）

3.【答案】B．考点：

1．单动点问题函数图象的分析；

2．由实际问题列函数关系式；

3．矩形的性质；

4．相似三角形的判定和性质；

．

4.【答案】1．考点：

1．圆周角定理；

2．相似三角形的判定和性质；

3．由实际问题列函数关系式；

3．二次函数的最值．

5.【答案】6．考点：

1．单动点问题；

2．轴对称的应用（最短路线问题）；

3．正方形的性质；

4．勾股定理．

（5题答图）（6题答图）

6.【答案】①③⑤．考点：

1．轴对称的性质；

2．垂直线段的性质；

3．圆周角定理；

4．含30度角直角三角形的性质；

5．等边三角形的性质；

6．切线的判定．

7.解：

（1）当PQ∥CD时，四边形PDCB是平行四边形，此时PD=QC，∴12﹣2t=t，∴t=4．

∴当t=4时，四边形PQDC是平行四边形．

（2）过D点，DF⊥BC于F，∴DF=AB=8．FC=BC﹣AD=18﹣12=6，CD=10，

①当PQ⊥BC，则BQ+CQ=18．即：

2t+t=18，∴t=6；

②当QP⊥PC，此时P一定在DC上，CP1=10+12﹣2t=22﹣2t，CQ2=t，易知，△CDF∽△CQ2P1，

∴，解得：

③情形：

当PC⊥BC时，因∠DCB＜90°

，此种情形不存在．

∴当t=6或时，△PQC是直角三角形．

8.解：

（1）.

（2）∵在整个运动过程中，点P移动的距离为cm，圆心移动的距离为cm，

∴由题意得①.∵点P移动2s到达B点，即点P用2s移动了cm，点P继续移动3s到达BC的中点，即点P用3s移动了cm，∴②.联立①②，解得.

∵点P移动的速度与⊙O移动的速度相等，∴⊙O移动的速度为（cm/s）.

∴这5s时间内圆心O移动的距离为（cm）.

（3）存在这样的情形.

设点P移动的速度为cm/s，⊙O移动的速度为cm/s，

根据题意，得.

如答图，设直线OO1与AB交于点E，与CD交于点E，⊙O1与AD相切于点PG.

若PD与⊙O1相切，切点为H，则.易得△DO1G≌△DO1H，∴∠ADB=∠BDP.

∵BC∥AD，∴∠ADB=∠CBD.∴∠BDP=∠CBD.∴BP=DP.

设cm，则cm，cm，在中，由勾股定理，得，

即，解得.∴此时点P移动的距离为（cm）.

∵EF∥AD，∴△BEO1∽△BAD.∴，即.∴cm，cm.

①当⊙O首次到达⊙O1的位置时，⊙O与移动的距离为14cm.

∴此时点P移动的速度与⊙O移动的速度比为.∴此时DP与⊙O1恰好相切.

②当⊙O在返回途中到达⊙O1的位置时，⊙O与移动的距离为cm.

∴此时点P移动的速度与⊙O移动的速度比为.∴此时DP与⊙O1不可能相切.

【考点】单动点和动圆问题；

矩形的性质；

直线与圆的位置关系；

勾股定理；

相似三角形的判定和性质；

方程思想和分类思想的应用.

【分析】

（1）根据矩形的性质可得：

点P从A→B→C→D，全程共移动了cm.

（2）根据“在整个运动过程中，点P移动的距离等于圆心移动的距离”和“点P用2s移动了cm，点P用3s移动了cm”列方程组求出a，b，根据点P移动的速度与⊙O移动的速度相等求得⊙O移动的速度，从而求得这5s时间内圆心O移动的距离.

（3）分⊙O首次到达⊙O1的位置和⊙O在返回途中到达⊙O1的位置两种情况讨论即可.

1.【答案】B．【解析】试题分析：

当点P在AD上时，△ABP的底AB不变，高增大，所以△ABP的面积S随着