中考常见几何模型分析Word格式.docx

中考常见几何模型分析Word格式.docx

《中考常见几何模型分析Word格式.docx》由会员分享，可在线阅读，更多相关《中考常见几何模型分析Word格式.docx（26页珍藏版）》请在冰点文库上搜索。

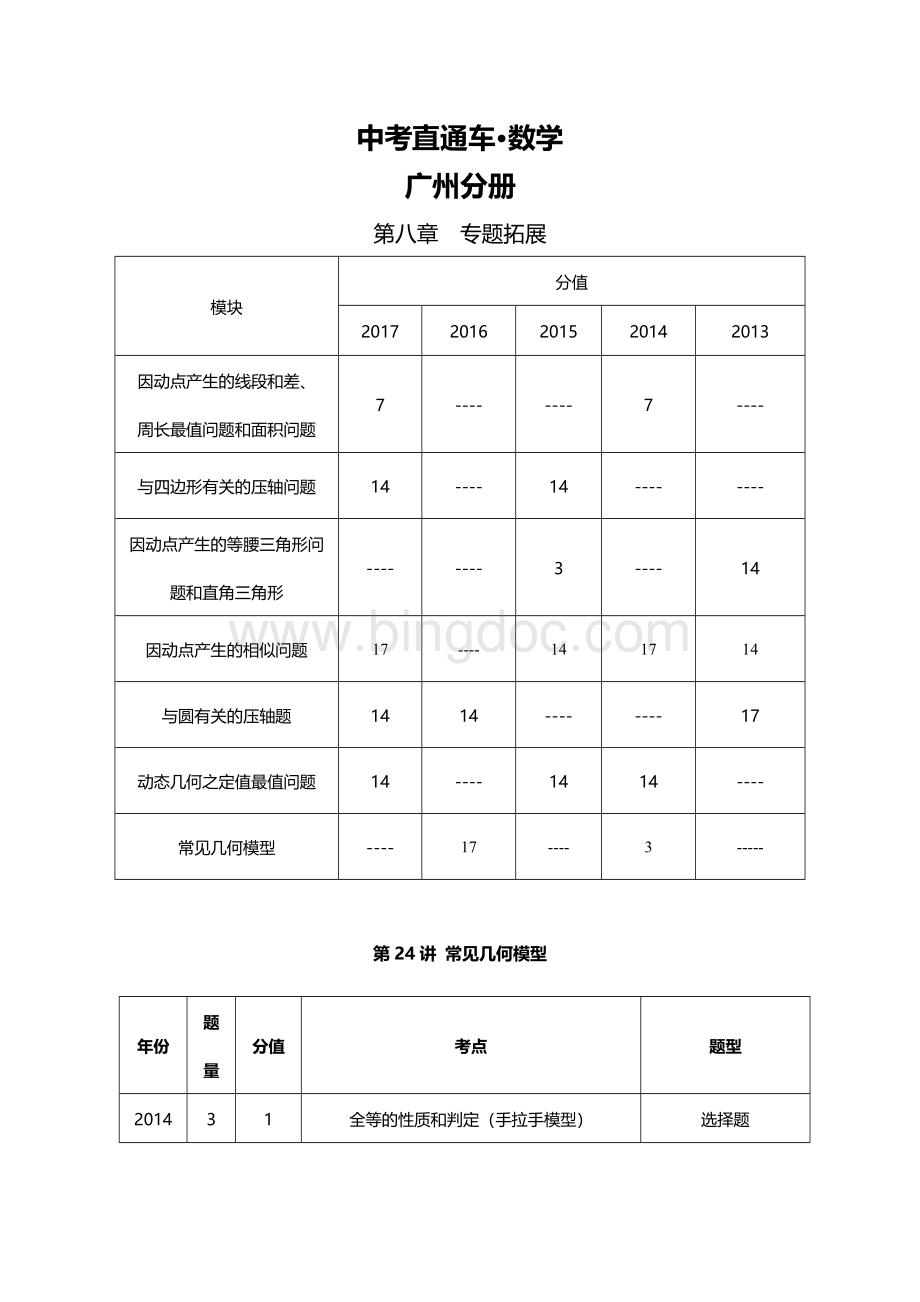
【结论】

（1）

（2）

（3）与之间的夹角为

（4）与的交点设为,

平分

2、【条件】如图两个等腰直角三角形与，连结,二者相交于点。

【结论】

（1）是否成立？

（2）=CE

（3）与之间的夹角为

（4）是否平分？

旋转模型：

一、邻角相等对角互补模型

【条件】如图，四边形ABCD中，AB=AD，

二、角含半角模型：

全等

角含半角要旋转：

构造两次全等

【条件】：

如图，点分别是正方形的边上的点，，连接；

（1）

（2）；

一线三等角模型:

【条件】一条直线同一侧三个相等的角（如图）；

1、锐角形一线三等角2、直角形一线三等角

3、钝角形一线三等角

【真题拾遗】

1．（2014•广州）如图，四边形ABCD、CEFG都是正方形，点G在线段CD上，连接BG、DE，DE和FG相交于点O，设AB=a，CG=b（a＞b）．下列结论：

①△BCG≌△DCE；

②BG⊥DE；

③=；

④（a﹣b）2•S△EFO=b2•S△DGO．其中结论正确的个数是（　　）

A．

4个

B．

3个

C．

2个

D．

1个

2．（2016•广州）如图，正方形ABCD的边长为1，AC，BD是对角线．将△DCB绕着点D顺时针旋转45°

得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．则下列结论：

①四边形AEGF是菱形 ②△AED≌△GED ③∠DFG=112.5°

④BC+FG=1.5

其中正确的结论是　　．

三、解答题

3．（2011广州中考）如图1，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°

，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上．

（1）证明：

B、C、E三点共线；

（2）若M是线段BE的中点，N是线段AD的中点，证明：

MN=OM；

（3）将△DCE绕点C逆时针旋转α（0°

＜α＜90°

）后，记为△D1CE1（图2），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1=OM1是否成立？

若是，请证明；

若不是，说明理由．

4．（2016广州中考）如图，点C为△ABD的外接圆上的一动点（点C不在上，且不与点B，D重合），∠ACB=∠ABD=45°

（1）求证：

BD是该外接圆的直径；

（2）连结CD，求证：

AC=BC+CD；

（3）若△ABC关于直线AB的对称图形为△ABM，连接DM，试探究DM2，AM2，BM2三者之间满足的等量关系，并证明你的结论．

参考答案

一、选择题

1、C

考点：

相似三角形的判定与性质；

全等三角形的判定与性质；

正方形的性质．

分析：

由四边形ABCD和四边形CEFG是正方形，根据正方形的性质，即可得BC=DC，CG=CE，∠BCD=∠ECG=90°

，则可根据SAS证得①△BCG≌△DCE；

然后根据全等三角形的对应角相等，求得∠CDE+∠DGH=90°

，则可得②BH⊥DE．由△DGF与△DCE相似即可判定③错误，由△GOD与△FOE相似即可求得④．

解答：

证明：

①∵四边形ABCD和四边形CEFG是正方形，

∴BC=DC，CG=CE，∠BCD=∠ECG=90°

，

∴∠BCG=∠DCE，

在△BCG和△DCE中，

∴△BCG≌△DCE（SAS），

②∵△BCG≌△DCE，∴∠CBG=∠CDE，又∠CBG+∠BGC=90°

∴∠CDE+∠DGH=90°

，∴∠DHG=90°

，∴BH⊥DE；

③∵四边形GCEF是正方形，

∴GF∥CE，

∴=，

∴=是错误的．

④∵DC∥EF，∴∠GDO=∠OEF，∵∠GOD=∠FOE，∴△OGD∽△OFE，

∴=（）2=（）2=，∴（a﹣b）2•S△EFO=b2•S△DGO．故应选B

点评：

此题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定和性质，直角三角形的判定和性质．

二、填空题

2、①②③

三角形全等、三角形内角和、菱形

首先证明△ADE≌△GDE，再求出∠AEF、∠AFE、∠GEF、∠GFE的度数，推出AE=EG=FG=AF，由此可以一一判断．

∵四边形ABCD是正方形，

∴AD=DC=BC=AB，∠DAB=∠ADC=∠DCB=∠ABC=90°

，∠ADB=∠BDC=∠CAD=∠CAB=45°

，

∵△DHG是由△DBC旋转得到，

∴DG=DC=AD，∠DGE=∠DCB=∠DAE=90°

在RT△ADE和RT△GDE中，

∴AED≌△GED，故②正确，∴∠ADE=∠EDG=22.5°

，AE=EG，

∴∠AED=∠AFE=67.5°

，∴AE=AF，同理EG=GF，∴AE=EG=GF=FA，

∴四边形AEGF是菱形，故①正确，

∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°

，故③正确．

∵AE=FG=EG=BG，BE=AE，∴BE＞AE，∴AE＜，∴CB+FG＜1.5，故④错误

故答案为①②③．

本题考查正方形的性质、全等三角形的判定和性质、菱形的判定和性质、等腰直角三角形的性质等知识，解题的关键是通过计算发现角相等，学会这种证明角相等的方法，属于中考常考题型．

3、

（1）三点共线

（2）中位线、全等三角形（手拉手性质）（3）同

（2）

（1）根据直径所对的圆周角为直角得到∠BCA=90°

，∠DCE是直角，即可得到∠BCA+∠DCE=90°

+90°

=180°

；

（2）连接BD，AE，ON，延长BD交AE于F，先证明Rt△BCD≌Rt△ACE，得到BD=AE，∠EBD=∠CAE，则∠CAE+∠ADF=∠CBD+∠BDC=90°

，即BD⊥AE，再利用三角形的中位线的性质得到ON=BD，OM=AE，ON∥BD，AE∥OM，于是有ON=OM，ON⊥OM，即△ONM为等腰直角三角形，即可得到结论；

（3）证明的方法和

（2）一样．

∵AB是直径，

∴∠BCA=90°

而等腰直角三角形DCE中∠DCE是直角，

∴∠BCA+∠DCE=90°

，∴B、C、E三点共线；

（2）连接BD，AE，ON，延长BD交AE于F，如图1，

∵CB=CA，CD=CE，∴Rt△BCD≌Rt△ACE，∴BD=AE，∠EBD=∠CAE，

∴∠CAE+∠ADF=∠CBD+∠BDC=90°

，即BF⊥AE，

又∵M是线段BE的中点，N是线段AD的中点，而O为AB的中点，

∴，，ON∥BD，AE∥OM；

∴ON=OM，ON⊥OM，即△ONM为等腰直角三角形，

∴MN=OM；

（3）成立．

理由如下：

如图2，连接BD1，AE1，ON1，∵∠ACB﹣∠ACD1=∠D1CE1﹣∠ACD1，

∴∠BCD1=∠ACE1，又∵CB=CA，CD1=CE1，∴△BCD1≌△ACE1，

与

（2）同理可证BD1⊥AE1，△ON1M1为等腰直角三角形，

从而有M1N1=OM1．

本题考查主要三角形全等的判定和中位线的性质，熟练掌握手拉手模型，作为本题切入点，可以非常顺利的解决本题。

4、

圆的相关概念、等腰三角形、截长补短（旋转模型性质）、勾股定理

（1）要证明BD是该外接圆的直径，只需要证明∠BAD是直角即可，又因为∠ABD=45°

，所以需要证明∠ADB=45°

（2）在CD延长线上截取DE=BC，连接EA，只需要证明△EAF是等腰直角三角形即可得出结论；

（3）过点M作MF⊥MB于点M，过点A作AF⊥MA于点A，MF与AF交于点F，证明△AMF是等腰三角形后，可得出AM=AF，MF=AM，然后再证明△ABF≌△ADM可得出BF=DM，最后根据勾股定理即可得出DM2，AM2，BM2三者之间的数量关系．

解：

（1）∵=， ∴∠ACB=∠ADB=45°

∵∠ABD=45°

， ∴∠BAD=90°

， ∴BD是△ABD外接圆的直径

（2）在CD的延长线上截取DE=BC，

连接EA， ∵∠ABD=∠ADB， ∴AB=AD，

∵∠ADE+∠ADC=180°

， ∠ABC+∠ADC=180°

， ∴∠ABC=∠ADE，

在△ABC与△ADE中，

， ∴△ABC≌△ADE（SAS）， ∴∠BAC=∠DAE，

∴∠BAC+∠CAD=∠DAE+∠CAD， ∴∠BAD=∠CAE=90°

， ∵= ∴∠ACD=∠ABD=45°

， ∴△CAE是等腰直角三角形， ∴AC=CE， ∴AC=CD+DE=CD+BC；

（3）过点M作MF⊥MB于点M，过点A作AF⊥MA于点A，MF与AF交于点F，连接BF，

由对称性可知：

∠AMB=ACB=45°

∴∠FMA=45°

∴△AMF是等腰直角三角形，

∴AM=AF，MF=AM，

∵∠MAF+∠MAB=∠BAD+∠MAB，

∴∠FAB=∠MAD，

在△ABF与△ADM中，

， ∴△ABF≌△ADM（SAS），

∴BF=DM， 在Rt△BMF中， ∵BM2+MF2=BF2， BM2+2AM2=DM2．

本题考查圆的综合问题，涉及圆周角定理，等腰三角形的性质，全等三角形的性质与判定，勾股定理等知识，熟练掌握旋转模型的特征和性质，作为本题切入点，构造出等腰直角三角形，方向明确，减小了本题的难度。

【模拟演练】

图2

1、（2014番禺华附一模）如图2，在矩形ABCD中，E为AD的中点，EF⊥EC交边AB

于F，连FC，下列结论不正确的是（D）．

A．AB≥AEB．△AEF∽△DCE

C．△AEF∽△ECFD．△AEF与△BFC不可能相似

2、（2017十六中一模）如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°

＜θ＜90°

），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是（C）．

（1）EF=2OE；

（2）S四边形OEBF：

S正方形ABCD=1：

4；

（3）BE+BF=2OA；

（4）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=34；

（5）OG•BD=AE2+CF2．

A.

（1）（3）（4）（5）B.

（2）（3）（4）（5）

C.

（1）

（2）（3）（5）D.

（1）

（2）（3）（4）

3、（2016黄埔区一模）如图，已知和均为等边三角形，点在边上，与相交于点，如果，，那么的长度为．

第4题

4、（2016荔湾区一模）如图，正三角形ABC内接于⊙O，P是弧上的一点（P不与点B、C重合），且，交于E，点F是延长线上的点，，，．

（1）求证≌；

（2）求证；

（3）求和的长．

5、（2016海珠区一模）已知正方形ABCD和正方形CEFG，连接AF交BC于O点，点P是AF的中点，过点P作PH⊥DG于H，CD=2，CG=1。

（1）如图1，点D、C、G在同一直线上，点E在BC边上，求PH得长；

（2）把正方形CEFG绕着点C逆时针旋转（0°

＜a＜180°

）

图（3）

①如图2，当点E落在AF上时，求CO的长；

图

（1）

图

（2）

②如图3，当DG=时，求PH的长。

6、（2017二中一模）已知抛物线C1：

经过点A（1，0）和B（-3，0）．

（1）求抛物线C1的解析式，并写出其顶点C的坐标；

（2）如图1，把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2，此时点A，C分别平移到点D，E处．设点F在抛物线C1上且在x轴的上方，若△DEF是以EF为底的等腰直角三角形，求点F的坐标；

（3）如图2，在

（2）的条件下，设点M是线段BC上一动点，EN⊥EM交直线BF于点N，点P为线段MN的中点，当点M从点B向点C运动时：

①tan∠ENM的值如何变化？

请说明理由；

②点M到达点C时，直接写出点P经过的路线长．

25题图1

25题图2

1、D

相似三角形、三角形内角和（一线三直角）

利用等角的余角相等得到∠AFE=∠DEC，则根据有两组角对应相等的两个三角形相似得到Rt△AEF∽Rt△DCE，由相似的性质得CD：

AE=DE：

AF，而CD=AB，DE=AE，则AB：

AE=AE：

AF，即AE2=AB•AF，利用AF≤AB，得到AB≥AE；

再利用Rt△AEF∽Rt△DCE得到EF：

EC=AF：

DE，把DE=AE代入得到EF：

AE，根据比例性质得EF：

AF=EC：

AE，加上∠A=∠FEC=90°

，则根据两组对应边的比相等且夹角对应相等的两个三角形相似得到△AEF∽△ECF；

由∠EFC≠90°

可判断△AEF∽△BFC相似不成立，而当∠AFE=∠BFC时，可判断△AEF∽△BCF．

∴∠AEF+∠DEC=90∘，∵∠AEF+∠AFE=90∘，∴∠AFE=∠DEC，

∴Rt△AEF∽Rt△DCE；

∴CD:

AE=DE:

AF，∵E为矩形ABCD的边AD的中点，

∴CD=AB，DE=AE，∴AB:

AE=AE:

AF,即AE2=AB⋅AF，

而AF⩽AB，∴AB⩾AE；

∵Rt△AEF∽Rt△DCE，∴EF:

EC=AF:

DE，而DE=AE，

∴EF:

AE，即EF:

AF=EC:

AE，∵∠A=∠FEC=90∘，∴△AEF∽△ECF；

∵∠EFC≠90∘∴△AEF∽△BFC相似不成立，

但当∠AFE=∠BFC时,△AEF∽△BCF.故选D.

此题为非常明显的考查相似三角形知识点，根据一线三等角模型特征快速得出答案。

2、C

正方形的性质，全等三角形的判定与性质，旋转的性质，相似三角形的判定与性质

①由四边形ABCD是正方形，直角∠MPN，易证得△BOE≌△COF（ASA），则可证得结论；

②由

（1）易证得，

则可证得结论；

③首先设AE=x，则BE=CF=1-x，BF=x，继而表示出△BEF与△COF的面积之和，然后利用二次函数的最值问题，求得答案；

④易证得△OEG∽△OBE，然后由相似三角形的对应边成比例，证得OG•OB=OE2，再利用OB与BD的关系，OE与EF的关系，即可证得结论．

①∵四边形ABCD是正方形，

∴OB=OC,∠OBE=∠OCF=45∘,∠BOC=90∘，∴∠BOF+∠COF=90∘，

∵∠EOF=90∘，∴∠BOF+∠COE=90∘，∴∠BOE=∠COF，

在△BOE和△COF中，∠BOE=∠COF，OB=OC

∠OBE=∠OCF，∴△BOE≌△COF（ASA），∴OE=OF，BE=CF，

∴EF=OE;

故正确;

②∵

∴；

故正确；

③过点O作OH⊥BC，∵BC=1，∴OH=12BC=12，

设AE=x，则BE=CF=1−x，BF=x，

∴

∵a=−12<

0，

∴当x=14时,最大；

即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=14；

故错误；

④∵∠EOG=∠BOE,∠OEG=∠OBE=45∘，

∴△OEG∽△OBE，

∴OE:

OB=OG:

OE，

∴∵OB=BD,OE=EF，

∴，

∵在△BEF中,，

∴.故正确。

故选C.

从图形上看是一个比较复杂的题，但是实际题目难度并不是很大，利用对角互补旋转模型结论再结合个够定理就能解决此题。

相似三角形的判定与性质,等边三角形的性质

先利用等边三角形的性质得到∠C=∠ADE=∠B=60°

，AB=BC=AC=12，再利用三角形外角性质证明∠BDF=∠CAD，则可判断△DBF∽△ACD，然后利用相似比计算BF的长．

∴∠C=∠ADE=∠B=60∘，AB=BC=AC=12，

∵∠ADB=∠DAC+∠C，

而∠ADB=∠ADE+∠BDF，

∴∠BDF=∠CAD，

∴△DBF∽△ACD，

∴BF:

CD=BD:

AC，

即BF:

4=8:

12,解得BF=.

故答案为.

此题利用对角互补旋转模型推导过程得到对应结论，再利用相似解决第

（2）（3）问

圆周角定理，等边三角形的性质，等边三角形的判定，圆内接四边形的任何一个外角都等于它的内对角

对于

（1），先根据等边三角形的性质得到AB=AC，再利用圆的内接四边形的性质得∠ACF=∠ABP，根据“SAS”即可得证；

对于

（2），先根据等边三角形的性质得到∠ABC=∠ACB=60°

，再根据圆周角定理得∠APC=∠ABB=60°

，加上∠CAE=∠PAC，于是可判断△ACE∽△APC，然后利用相似比即可得到结论；

对于（3），先利用计算出AE=，则PE=AP-AE=，再证△APF为等边三角形，得到PF=PA=4，则有PC+PB=4，接着证明△ABP∽△CEP，得到PB·

PC=PE·

AP=3，然后根据根与系数的关系，可把PB和PC看作方程的两实数解，再解此方程即可得到PB和PC的长.

∵正三角形ABC内接于⊙O，

∴AB=AC.

∵四边形ABPC为圆的内接四边形，

∴∠ACF＝∠ABP.

在△ABP和△ACF中，

∴△ABP≌△ACF.

（2）证明：

∴∠ABC＝∠ACE=60°

∴∠APC＝∠ABC=60°

∴∠ACE=∠APC

∵∠CAE=∠PAC

∴△ACE∽△APC

∴AE:

AC=AC:

AP

∴.

（3）∵，AB=AC，

∵△ABP≌△ACF，

∴∠APB=∠F=60°

.

而∠APC=60°

∴△APF为等边三角形，

∴PF=PA=4，

∴PC+CF=PC+PB=4.

∵∠BAP=∠PCE，∠APB=∠APC，

∴△ABP∽△CEP，

∴PB:

PE=AP:

PC，

∴PB·

AP=×

4=3.

∵PB+PC=4，

∴PB和PC可看作方程的两实数解，解此方程得.

∵PB＜PC，

∴PB=1，PC=3．

此题为标准手拉手模型，所以除了相似三角形得出答案，还能利用手拉手模型性质解决。

5

梯形中位线、相似三角形、勾股定理、全等三角形（一线三直角）

先判断出四边形APGF是梯形，再判断出PH是梯形的中位线，

得到；

（2）①先判断出△COE∽△AOB，得到AO是CO的2倍，设出CO，表示出BO，AO，再用勾股定理计算，②先找出辅助线，再判断出△ARD≌△DSC，△CSG≌△GTF，求出AR+FT，最后用梯形中位线即可．

（1）PH⊥CD，AD⊥CD，

∴PH∥AD∥FG，

∵点P是AF的中点，

∴PH是梯形APGF的中位线，

（2）①∵∠CEO=∠B=90∘，∠COE=∠AOB，

∴△COE∽△AOB，

∴COAO=CEAB，

∴COAO=12，

设CO=x，

∴AO=2x，BO=2−x，

在△ABO中,根据勾股定理得,，

∴或（舍），

∴CO=x=.

②如图3，

分别过点A，C，F作直线DG的垂线，垂足分别为R，S，T，

∵∠ADR+∠CDS=90∘,∠CDS+∠DCS=90∘，

∴∠ADR=∠DCS，

∵∠ADR=∠CSD=90∘，

∵AD=CD

∴△ARD≌△DSC，

∴AR=DS，

同理：

△CSG≌△GTF，

∴SG=FT，

∴AR+FT=DS+SG=DG=，

同

（1）的方法得，PH是梯形ARTF的中位线，

此题利用梯形中位线性质解决第

（1）问，第

（2）利用相似结合勾股定理这中常用方法求长度，第（3）问构造一线三直角模型解决问题。

6、

二次函数、等要直接三角形、相似三角形（一线三直接）、三角函数、中位线

（1）根据解析式求出坐标；

（2）根据等腰三角形的性质，EF=求出EF的长度，再根据抛物线与直线纵坐标差值求出答案。

（3）①根据答案需要求的正切值转换为相似比，再根据已知的两个直角构造出一线三直接模型，相似比为定值，②初中能解决的路径不是线段就是弧长，有关键位置分析可知轨迹为三角形中位线。

（1）∵抛物线C1：

经过点A（1，0）和B（-3，0），

∴解得，

∴抛物线C1的解析式为，

∵，

∴顶点C的坐标为（-1，-2）；

（2）如图，作CH⊥x轴于H，

∵A（1，0），C（-1，-2），

∴AH=CH=2，

∴∠CAB=∠ACH=45°

∴直线AC的解析式为y=x-1，

∵△DEF是以EF为底的等腰直角三角形，

∴∠DEF=45°

∴∠DEF=∠ACH，

∴EF∥y轴，∵DE=AC=2，∴EF=4，

设F（m，），则E（m，m-1），

∴EF=-（m+1）=4，解得m=±

3，

∵点F在x轴上方，∴F（3，6）.

（3）①tan∠ENM的值为定值，ta