第四章堆和不相交集数据结构.docx
《第四章堆和不相交集数据结构.docx》由会员分享,可在线阅读,更多相关《第四章堆和不相交集数据结构.docx(13页珍藏版)》请在冰点文库上搜索。
第四章堆和不相交集数据结构
第四章堆和不相交集数据结构
一、堆的定义
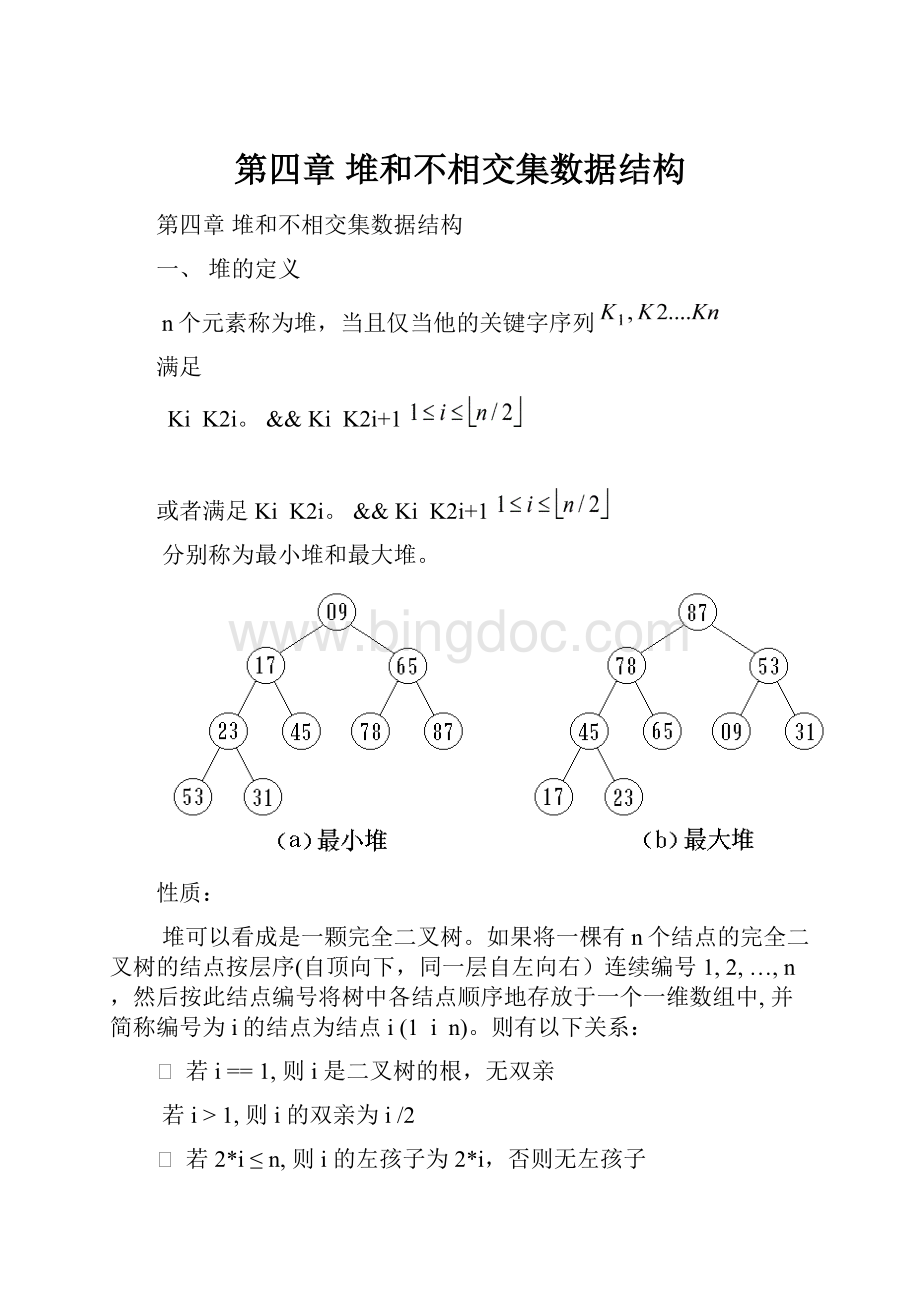
n个元素称为堆,当且仅当他的关键字序列
满足
KiK2i。
&&KiK2i+1
或者满足KiK2i。
&&KiK2i+1
分别称为最小堆和最大堆。
性质:
堆可以看成是一颗完全二叉树。
如果将一棵有n个结点的完全二叉树的结点按层序(自顶向下,同一层自左向右)连续编号1,2,…,n,然后按此结点编号将树中各结点顺序地存放于一个一维数组中,并简称编号为i的结点为结点i(1in)。
则有以下关系:
⏹若i==1,则i是二叉树的根,无双亲
若i>1,则i的双亲为i/2
⏹若2*i≤n,则i的左孩子为2*i,否则无左孩子
若2*i+1≤n,则i的右孩子为2*i+1,否则无右孩子
⏹i所在层次为logi+1
⏹若设二叉树的深度为h,则共有h层。
除第h层外,其它各层(0h-1)的结点数都达到最大个数,第h层从右向左连续缺若干结点
⏹具有n个结点的完全二叉树的深度为logn+1
二、堆上运算
在此考虑最大堆。
1.Sift-up:
把堆上的第i个元素上移;
2.Sift-down:
把堆上的第i个元素下移;
3.Insert:
把元素x插入堆中;
4.Delete:
删除堆中第i个元素;
5.删除最大元素
6.Makeheap:
创建堆;
7.Heapsort:
对排序;
1.过程Sift-up
输入:
数组H[1..n]和位于1和n之间的索引i
输出:
上移H[i](如果需要),以便使他不大于父结点(大堆)
Done←false
Ifi=1thenexit
Repeat
Ifkey(H[i])>key(H
)then互换H[i]和(H
elsedone←true
i←
untili=1ordone
例:
分析:
执行时间O(logn),空间
(1)
2.过程Sift-down
输入:
数组H[1..n]和位于1和n之间的索引i
输出:
下移H[i](如果需要),以便使他不小于子结点
Done←false
If2i〉nthenexit{节点是叶节点}
Repeat
i←2i
Ifi+1
nandkey(H[i+1])>key(H[i])theni←i+1
Ifkey(H
))和H[i]
elsedone←true
endif
until2i>nordone
例:
分析:
执行时间O(logn),空间
(1)
算法4.1insert
思想:
先插到最后,然后上移
输入:
堆H[1..n]和元素x
输出:
新的堆H[1…n+1],x为其元素之一
1.n←n+1{增加H的大小}
2.H[n]←x
3.Sift-up(H,n)
例:
分析:
执行时间O(logn),空间
(1)
算法4.2delete
思想:
先将最后元素替代H[i],然后调整
输入:
非空堆H[1..n]和位于1和n之间的索引i
输出:
删除H[i]之后的新堆H[1..n-1]
1.x←H[i];y←H[n];
2.n←n-1{减小H的大小}
3.ifi=n+1thenexit{完成}
4.H[i]←y
5.ifkey(y)
key(x)thensift-up(H,i)
6.elseSift-down(H,i)
7.endif
例:
分析:
执行时间O(logn),空间
(1)
deleteMAX
输入:
非空堆H[1..n]
输出:
返回最大键值元素x并从堆中删除
1.x←H[1]
2.Delete(H,1)
3.Returnx
创建堆
方法一:
假设从一个空堆开始,对数组中的n个元素,连续地使用insert操作插入堆中。
时间复杂度O(nlogn),
方法二:
直接在数组中进行调整,把数组本身建为一个堆。
算法4.4Makeheap
输入:
n个元素的数组A[1..n]
输出:
A[1..n]转换为堆
1.Fori←
downto1
2.Sift-down(A,i)
3.endfor
令A[j]对应树中第i层中第j个节点,Sift-down(A,j)最多调用k-i次,在第i层正好有
个节点,0
i=
=
Sift-down的每一个循环中,元素每下一层,需要有两次的比较,因此元素比较的总次数上界为4n.
每个节点做下移操作时,至少必须执行两次比较,共对
个节点做下移操作,因此需要2
n-1,所以Makeheap的时间复杂度为
(n)
堆排序
堆排序分为两个步骤:
第一步,根据初始输入数据,利用堆的调整算法形成初始堆,第二步,通过一系列的对象交换和重新调整堆进行排序。
基于初始堆进行堆排序
n最大堆的第一个对象r[1]具有最大的关键字,将r[1]与r[n]对调,把具有最大关键字的对象交换到最后,再对前面的n-1个对象,使用堆的调整算法HeapAdjust(1,n-1),重新建立最大堆。
结果具有次最大关键字的对象又上浮到堆顶,即r[1]位置。
n再对调r[1]和r[n-1],调用HeapAdjust(1,n-2),对前n-2个对象重新调整,…。
n如此反复执行,最后得到全部排序好的对象序列。
这个算法即堆排序算法。
算法4.5heapsort
输入:
n个元素的数组A[1..n]
输出:
以非降序排列数组
1.makeheap(A)
2.Forj←ndownto2
3.互换A[1]和A[j]
Sift-down(A[1…j-1,1)
4.endfor
分析:
建堆
,Sift-down运算用O(logn),重复n-1次,所以共用O(nlogn)
4.3不相交集数据结构
很多应用中,经常把n个元素划分为若干个集合,然后把某两个集合合并成为一个集合,或者寻找包含某个特定元素的集合。
Find(x):
寻找并返回包含某个特定元素x的集合的名字。
Union(x,y):
合并包含元素x和y的两个集合。
为实现这两个操作,需要一个简洁的数据结构。
将每个集合表示为一棵树,树中的每个结点表示集合中的一个元素,集合中元素x的值放在相应的树结点中。
非根的每个结点,都有一个指针指向父结点,根结点的父结点指针为空。
例:
{1,7,10,11},{2,3,5,6},{4,8},{9}
4.3.1按秩合并措施
为防止union操作中,树变化为退化树,在每个结点中存储一个非负数作为该结点的秩,记为rank,结点的秩基本就是它的高度。
Union运算法则:
设x和y是当前森林中两颗不同的树的根,初始状态时,每个结点的秩是0,执行union运算时,比较:
Rank(x)>rank(y),使x为y的父结点;
Rank(x)Rank(x)=rank(y),使y为x的父结点,并将rank(y)+1;
结论4.1:
rank(P(x))
rank(x)+1,p(x)为x的父结点
结论4.2:
rank(x)的初始值为0,在后继的合并运算序列中递增,直到x不再是根结点。
一旦x变成其他结点的子结点,他的秩就不再改变。
引理:
包括根结点在内的树中结点的个数至少是
。
证明:
用数学归纳法
(1)开始,x本身是一棵树,其秩rank(x)=0,其结点数
(2)假设x和y是两颗不同的树的根,其秩分别为如rank(x),rank(y)。
在执行union(x,y)操作之前,结点数分别是
和
。
在在执行union(x,y)操作之后,有三种情况:
●Rank(x)●Rank(x)>rank(y),同理;
●Rank(x)=rank(y),在执行union(x,y)操作前,两颗树节点数至少为
=
;在执行union(x,y)操作后,新树的节点数至少为2*
=
。
若新树以y为根,则y的秩增加1,否则新树以x为根,则x的秩增加1,两种情况都成立。
证毕
4.3.2路径压缩
为进一步提高find操作的性能,可采用路径压缩方法。
在find操作中找到根结点y之后,再沿着这条路径,改变路径上所有结点的父结点指针,使其直接指向y。
路径压缩虽然增加了find的执行时间,但路径缩短了,以后执行find操作会节省时间。
4.3.3union-find算法
算法4.6find
输入:
结点x
输出:
root(x),包含x的树的根
1.y←x
2.whilep(y)≠null{寻找包含x的树的根}
3.y←p(y)
4.endwhile
5.root←y;y←x;
6.whilep(y)≠null{执行路径压缩}
7.w←p(y)
8.p(y)←root
9.y←w
10.endwhile
11.returnroot
结论:
find操作的执行时间是
O(logn)
算法4.7union
输入:
两个元素x和y
输出:
包含x和y的两个树的合并,原来的树被破坏
1.u←Find(x);v←Find(y)
2.ifrank(u)≤rank(v)then
3.p(u)←v
4.ifrank(u)=rank(v) thenrank(v)←rank(v)+1
5.elsep(v)←u
6.endif
结论:
union操作的执行时间也是O(logn)
因为union操作除了执行两次find操作外,其余花费O
(1)时间。