插值数值分析.docx

资源描述

插值数值分析.docx

《插值数值分析.docx》由会员分享，可在线阅读，更多相关《插值数值分析.docx（38页珍藏版）》请在冰点文库上搜索。

插值数值分析.docx

插值数值分析

§1.0弓I言

众所周知，反映自然规律的数量关系的函数有三种表示方法:

A.解析表达式

f（x）=x_2x_5.

（开普勒（Kepler）方程）x=y-；siny.。

悬链线方程：

y二，cos（x/）。

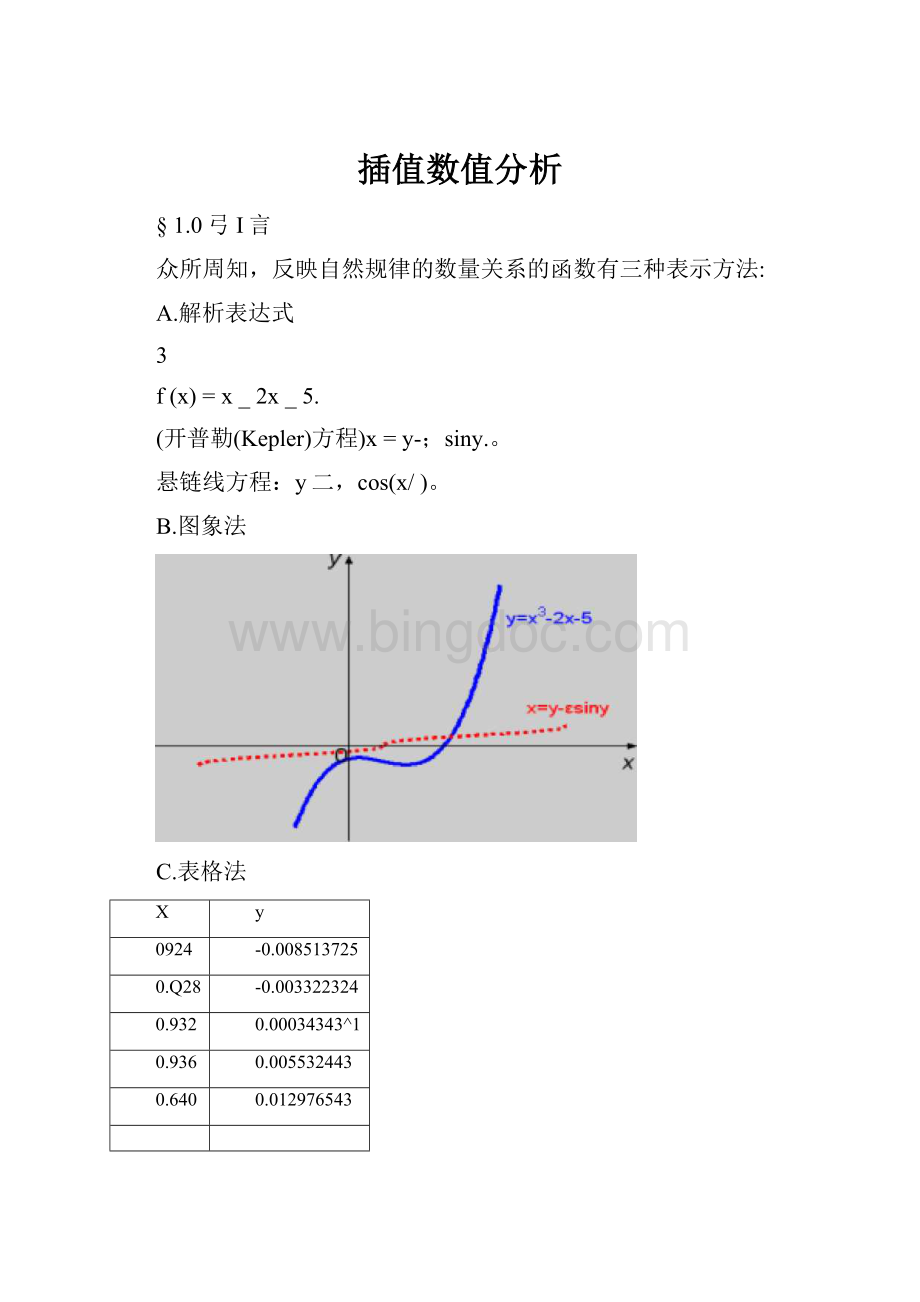
B.图象法

C.表格法

0924

-0.008513725

0.Q28

-0.003322324

0.932

0.00034343^1

0.936

0.005532443

0.640

0.012976543

2、事实上，许多数据都是用表格法给出的（如观测和实验而得到的函数数据表格），可是，从一个只提供离散的函数值去进行理论分析和进行设计，是极不方

便的甚至是不可能的。

因此需要设法去寻找与已知函数值相符，并且形式简单的

插值函数（或近似函数）。

3、另外一种情况是，函数表达式完全给定，但其形式不适宜计算机使用，因为计算机只能执行算术和逻辑操作，因此涉及连续变量问题的计算都需要经过离散化以后才能进行。

如数值积分方法、数值微分方法、差分方程以及有限元法等。

对于实际中的这些复杂函数，希望能构造一个既能反映函数本身的特性，又便于计算的简单函数，近似替代原来的函数。

有两种方法解决上述问题：

1、插值法对于一组离散点（xi，f（xj）,（i=0,1,2,...,n），选定一个便于计算的简单函数P（x），如多项式函数，要求P（x）满足P（xJ二f（xj，由此确定函数P（x）作为f（x）的近似函数，然后通过处理P（x）获得关于f（x）的结果。

这就是插值方法。

是广泛应用于理论研究和生产实践的重要数值方法，它是用简单函数（特别是多项式或分段多项式）为各种离散数组建立连续模型；为各种非有理函数提供好的逼近方法。

2、曲线拟合选定近似函数P（x）时，不要求近似函数P（x）必须满足P（xJ二f（xj，而只要求在某种意义下（最小二乘法原理），使近似函数P（x）在这些点上的总偏差量最小，这类方法成为曲线拟合。

§1.1多项式插值问题的一般提法

1插值法的概念：

假设函数y=f（x）是［a,b］上的实值函数，xo,xi,,,xn是［a,b］上n+1个互异的点，f（x）在这些点上的取值分别为y。

yi,,,yn,求一个确定的函数P（x）,使之满足：

P（xj=yi（i=0,1,2,,,n）⑴

称xo,xi,,,xn为插值节点，关系式

（1）称为插值原则，函数P（x）称为函数y=f（x）的插值函数，区间［a,b］称为插值区间。

插值函数p（x）作为f（x）的近似，可以选自不同类型的函数，女口p（x）为代数多项式、三角多项式等；其函数性态可以是光滑的、亦可以是分段光滑的。

其中，代数多项式类的插值函数占有重要地位：

（a）结构简单、计算机容易处理、任何多项式的导数和积分也易确定，并且仍是多项式。

（b）著名的Weierstrass逼近定理（定义在闭区间上的任何连续函数f（x）,

存在代数多项式p（x）一致逼近f（x）,并达到所要求的精度.）o

因此，我们主要考虑代数多项式的插值问题。

2泰勒插值：

人们熟悉的泰勒展开方法其实就是一种插值方法，泰勒多项式：

'f（x0）2fn（x0）n/、

Pn（X）二f（X。

）f（X°）（X-X。

）-（X-X°）-...-（X-X°）

（1）

与f（x）在点Xo邻近会很好的逼近f（x）o

泰勒余项定理：

定理1假设f（x）在含有点Xo的区间［a,b］内有直到n+1阶导数，则当x［a,b］时，对于式

（1）给出的Pn（x），成立

fn卅（d

f（x）-Pn（x）二/J（X-Xo）n1

（n+1）!

其中•介于Xo与x之间，因而［a,b］o

所谓泰勒插值指下述问题：

问题1求作n次多项式Pn（x），使满足Pn"k）（Xo）=yok）,k=0,1,2,...,n，yok）为一组已给数据。

易看出，上述插值问题的解就是泰勒多项式

（1）o

例1例题分析：

求作f（x）x在xo-100的一次和二次泰勒多项式，利用它们计算.115的近似

值并估算误差。

解:

f（x".X,

'1.1/2

f（x）x,

f'（x。

）=1/20,

x。

=100的一次泰勒多项式是

”1」/2

f（x）x,

f（X0）=10,

f（x）=X在

R（x）=f（x0）+f（x0）（x-x0）=5+0.05xx=115时^115=f（115）俺R（X）=10.75根据定理1可估计误差

--f''（E）——2

（X—X°）<

42討“

f"（x0）=—1/4000,f''（x0）=3/8000000

f（X。

）一

（x-X0）2c0.028125c0.05

2'…2

误差小于十分位的一半，故十分位及前面的数字为有效数字，所以结果有三位有效数字。

修正R（x）可进一步得到二次泰勒公式

f''（X0）2

P2（x）二R（x）2（x-x。

）

.115二f（115）：

P2（X）=10.75-0.028125=10.721875

mj.

f（）

2、_2

误差小于百分位的一半，故百分位及前面的数字为有效数字，所以结果有四位有效数字。

泰勒插值是一种有效的插值方法，对函数要求严格（要足够光滑，存在高阶导数），要计算函数的高阶导数，而高阶导数的计算对计算机来说就很困难；另外,计算过程不能形成机械重复的过程，不利于计算机程序实现。

§4.2拉格朗日（Lagrange）插值

1多项式插值的存在惟一性：

多项式导数易于计算，函数表达式简单，计算机易于计算，故考虑用多项式函数作为插值函数来模拟实际函数。

从如下数据表着手,并假定XiXj,0-ij-n，

f（x）—Pi（x）=

f（x）—P2（X）=

（x—x。

）3:

f（X。

）

（x-x0）‘：

：

0.0006328125：

：

0.005

X0X1X2…Xn

y0y1y2…yn

求n次多项式^（x）—a0a1Xanx,使得:

P（Xi）=yi（i=0,1,2,,,n）。

根据插值条件，有：

=yo

nanXi二yi

P（x。

）=a0aiX。

anXoP（Xi）=ao+aiXi

注意到插值节点Xi（i=人2,，n）两两相异，而

Vn（Xo,Xi,,Xn）（Xj-Xj）=0

0当匕弐

故方程组（i）有惟一解a0，ai「an,于是满足插值条件的多项式存在且惟一。

定理由n+i个不同插值节点X0，Xi，，Xn可以惟一确定一个n次多项式

Pn（x）二aoaiX•…•anXn满足插值条件Pn（Xi）二%。

从理论上说，由方程组⑴可以求出a0,aH可的惟一解，从而确定Pn（X）。

但从数值计算上看，当n较大时求解线性方程组的工作量较大且不便应用。

解方程组（i）需计算n+i个n阶行列式，每个n阶行列式为n!

项之和，每项又是n个元素的乘积，需n-i次乘法，所以求解需要（ni）n!

（n-1）次乘法，当n较大时，计算量非常大。

为解决此问题，现已提出了不少构造Rd）的巧妙办法。

2Lagrange插值的基函数构造法

首先讨论n=1时的情形。

已知Xo,Xi；yo,yi，求Li（x）-a。

aiX使得Li（Xo）=yo;L|（xj=yi

显然Li（x）是过（Xo,yo）和（xi,yi）两点的一条直线

roxTx

由点斜式容易求得

LSyo；二八）

lo（XoP1；lo（XiP0

li（XoPO;li（Xip1

称其为线性插值基函数。

L1（X）可以通过函数li（X）,（Ho,1）组合得出，且组

合系数恰为所给数据yo,y10

例题

a）利用100,121的开方计算115

解：

由于

100

121

7‘X

利用Lagrange插值法有

于是,

=10.71428

115的准确值为10.72380529,,因此近似值10.71428有3位有效数字

再讨论n=2时的情形

Xo,X1,X2

已知y0,y1,y2，求L2（x）

使得

L2（xo）-y0；L2（x1）-y1；L2（X2）-y2

于是,

（X-xj（x-X2）L2（x）--yo

（x°-x-）（x°-X-）

（x-xo）（x-x-）y

'h（x）yi

i=0

（x^~X°）（X--X-）1

（X-Xo）（X-X-）y

（X--X°）（x--X-）2

最后讨论一般情形。

X-…Xn

y。

y-…yn

求Ln（x）使得L（Xi）=yi（i=0,1,2,,,n）。

令n次多项式插值基函数为：

n（X-Xj）li（x）-

需（Xi-Xj）

h（x）,（i二

0-,,n）具有如下特点：

1,i二j“（i,j=0,1，…,n）

10,"j。

于是，满足插值条件的n次多项式可以直接写为：

nn（X-Xj）n

Ln（x）乜八h（x）yi

Inj护（Xj一Xi）In

j=0'Ij7

我们称Ln（x）为Lagrange多项式，li（X）

^其Lagrange插值基函数。

结束

思考给定Xi=i+1,i=0,1,2,3,4,5.下面哪个是12（x）的图像?

牛ABtC

3插值余项

如图所示，其截断误差R（x）=f（x）-Ln（x）,称为Lagrange插值多项式的余项

xo，X1，，xn取值为f（N）yi,Ln（X）是经过插值样点（Xi,yi）,（i=0,1,…，n）的

Lagrange插值多项式，若引进记号：

n1（X）=（X—Xo）（X-Xj（X—Xn）二川（X—Xi）

i=0

（n1）

则当x，［a,b］时，有如下的误差估计：

・G）nRn（x）二f（x）-Ln（x）二：

J【（x-x）

n1（X）（a,b）

（n+1）!

f"「）

（n+1）!

证明：

因为&（凶）=f（X）一Ln（X）0（^0,1/,n）于是可假定Rn（X）具有如下形式：

Rn（x）=k（x）（x-Xo）（x-Xi）…（x-Xn）=k（x）叮（x-x）

i=0

将x看作（a,b）上的一个固定点，作辅助函数

®（t）=f（t）-Ln（t）-k（x）（t-X°）（t-Xi）…（t-Xn）

二f（t）-Ln（t）-k（X）i【（t-Xi）

i=0

容易看出，-（t）有x，Xo,Xi，…，Xn共n+2个相异零点,且在［a,b］上存在n+1阶导数。

根据罗尔，「（t）在‘（t）的两个零点之间至少有一个零点，故：

（t）在［a,b］上至少有n+1个零点。

如此类推J"1）（t）在（a,b）上至少有1个零点，使得

（n1）n

（n1）（）=f（n1）（）-L（nn1）（）-k（x）加m）t-

dti=0

注意到L是n次多项式，L（nn1）（t）=0；JF）的首项为厂，

d（nd）n

（n1）

故dt（nX卫（t_Xi）=（nT）!

。

由上述方程解得f（n杓（巴）

k（x）—穿（a,b）

（n1）/-

（n+1）!

。

Rn（x）=n（x^x）

于是

（n+1）!

（n1）/

如果f（x）在（a,b）上有界，即

弓M>O」fE（x）卜M,$x亡（a,b）

则有余项估计:

因此，插值多项式Ln（x）对于次数岂n的多项式的估计是精确的。

即插值函数就是它本身。

（1）

思考:

线性插值的余项估计：

冋&）|兰（儿xo）max|f（x）|

8Xo$$1

（2）抛物线插值的余项估计：

f”牡）弦

R2（X）|^（x・Xo）（x]X1）（x]X2）d亡[xo，x2]

4误差事后估计

如果没有给出f（x）的表达式，只提供了离散值，无法直接用余项公式，这里介绍另一种误差分析方法。

考察三个节点X0,X1,X2，对于给定插值点X，分别用线性插值求出f（x）的两个近似值，由余项定理

f"（%）

y-%（x-x°）（x-X1）

"2J[2）（x-X°）（X-X2）

；1,；2[a,b]，假设f"（x）在[a,b]变化不大，两式相除得：

插值结果y1的误差y-力可通过两次插值的偏差（y?

-yj来估计

例p21

5例题

例1已知函数y=f（x）的观察数据为

-2

P01

-3

试构造f（X）的拉格朗日多项式Ln（X），并计算f（-1）解先构造基函数

x（x-4）（x-5）x（x-4）（x-S）

（-2-0）（-2-4）（-2—5）84

（j+2）0-4）（疋一5）_O+2〕0-4）0一5）（0—（—2））（0—4）（0—3）一40

/2«=

4（X）二

（x+2）x（x-5）x（x+2）（x-5）

（4+2）（4-0）（4-5）一24

（x+2）x（x-2）（x-4）_（a+2）x（x-4）（5+2）（5—0）（5—4）-35

所求三次多项式为

2＞恥）

L3（X）=

_5双一4）（一5）（工+2）（一4）（一5）

二胡+■■:

（_3）x^+2）（x-5）（x+2）x（x-4）

24+

—Xs-—X2-—X+1

421421

5155.

L3（-1）二-L）二

例2已知连续函数f（x）=1/x,其函数表如下:

x22.54

f（x）0.50.40.25

求方程f（3）的值并估计误差。

解：

利用Lagrange插值法有

（x-2.5）（x-4）

（2-2.5）（2-4）

（x「2）（x「4）（0.4）（2.5-2）（2.5-4）（x2）（x2.5）（0.25）（4-2）（4-2.5）

-0.425x1.15

-0.05x2

故f（3）L2（3）=0.325。

因为

0.03125

实际误差

总结：

尽管抛物插值的精度比线性插值好，但并不能认为插值多项式的次数n越高越好。

因为当n较大时，常有数值不稳定的现象，特别当n很大时时，插值函数并不一定收敛到被插函数f（x）o所以，一般你n<7,否则采用分段低次插值的方法。

Lagrange插值法非常适合用计算机求解，但是，如果需要增加一个插值节点，则Lagrange插值公式的所有系数需要重新计算，会造成计算量的浪费！

有没有具有承袭性的公式，答案是肯定的，埃特金插值和牛顿插值就是这样的。

埃特金插值将一个高次的插值过程归结为线性插值的多次重复，逐步提高插值次数。

§4.3差商与差分及其性质

差商的概念:

特别地，定义f[XoHf（Xo）为函数f（X）关于Xo的零阶差商。

由此可知，高阶差商总是由比它低一阶的的两个差商组合而成。

该性质说明：

k阶差商f[Xo，^，…，Xn]计算是由函数值f（xo）,f（Xi）,,f（Xk）线性组合而。

如：

f[Xo,Xi,X2】=f[Xi,Xo,X2】=f[X2,Xi,X°]；

（b）性质2（对称性）:

差商与节点的顺序无关。

即

f[Xo,Xi]=f[Xi,Xo]

f[X）,Xi,X2]二f[Xi,Xo,X2]二f[Xo,X2,Xi]

这一点可以从性质1看出

3利用差商表计算差商

利用差商的递推定义，可以用递推来计算差商差商表：

f（xj

一阶差商

二阶差商

三阶差商

f（Xo）

f（Xi）

f【Xo,Xi]

f（X2）

fIx1,X2]

f〔Xo，Xi，X2】

f（X3）

fIX2,X3]

f[Xi,X2,X3〕

f[x°,Xi,X2,X3]

如要计算四阶差商，应再增加一个节点，表中还要增加一行例1:

已知

f（Xi）

计算二阶差商f[1，2，，7]

解：

列表计算

f（Xi）

一阶差商

二阶差商

三阶差商

-1

-3.5:

-1.25

分别为f（x）在xi处以h为步长的一阶向前差分，一阶向后差分和一阶中心差分称符号△、▽、S分别为向前差分算子，向后差分算子和中心差分算子。

X.2一x.

=*（亦02水旳

差分表

y。

•詡。

y。

在节点等距情况下，差商可用差分表示，设步长h=x.“-X.，有

x.1-x.h

f（X|,Xi）」（Xl）-f（X|）亠

般形式

§4.4牛顿插值公式

1.牛顿插值公式的构造

Lagrange插值虽然易算，但若要增加一个节点时，全部基函数li（x）都需

重新算过。

本节介绍另外一种方法-牛顿插值法，并用它解决上面所述问题。

将Lagrange插值公式

nn（X-Xjn的=.毗鳥3”

由线性插值

Ni（x）=y°yiy°（x-X。

），令a。

=y。

◎=yiy°,Ni（x）=a。

ai（x-x。

）

Xi-XgXi—X。

二次插值能否写成

N2（x）二a。

y（x-Xo）a2（x-Xo）（x-xj

由条件N2（x°）=丫0小2（&）=%,N2（X2）=y2得

y2-y0yi-y0

a^yo,a^y1~yo,a2

xi—xo

X2-x。

Xi-Xo

X2_Xr

推广得

Nn（x）二a。

®（x-x。

）a?

（x-Xo）（x-xj…a.（x-X。

）…（x-X-i）

其中，ao,ai,,an为待定系数。

如何求a。

，*1，,an

f[x,x。

"空匕週

因为X-X。

所以f（x）=f（X。

）f[x,xj（x-Xo）（0）

f[x,X。

]-f[Xo,Xi]

f[X,Xo,Xi]

又X_Xi,有

f[X,Xo]=f[XoN]f[X,Xo,Xd（X-xj（i）

又

解:

f[x,x。

凡xjJXM-%"』

f[X,X0,Xj=f[X0,片,X2]f[X,Xo,片,X2】（XX2）

（2）

-般地,f[X，X0,111,Xn]

_f[X,Xo,,Xn_i]-f[Xo，X!

，,Xn]X_Xnf[X,Xo,,Xn“二f[Xo，X!

川，Xn]f[X,Xo，lll,Xn]（XXn）

将式（n）代入式（n-i）,...,式⑵代入式（i）,式（i）代入式（0）,

如此可得：

（n）

f（x）=f（X。

）f[Xo，X』（XXo）

f[Xo,Xi,X2】（XX°）（XXi）III

+f[x0,x1J||,x1]（xX）lll（xX_i）

+f[HX）,X川,Xj（x"）（xX）川（xXi）

尤为注意的是：

最后一项中,差商部分含有X,乃是余项部分,记作Rn（x）；而前面n+1项中,差商部分都不含有X,因而前面n+1项是关于X的n次多项式,记作Nn（x）,这就是牛顿插值公式。

于是，上式成为f（小Nn（X）Rn（x）。

2算例

例1:

当n=1时，

f（X）=f（Xj+f[Xo,Xi]（X-X。

）+f[X,Xo,Xi]（X-X°）（X-X」

其中,'

Ni（x）二f（Xo）f[Xo,Xi]（X-Xo）

“0宝如-冷）

X。

这就是牛顿一次插值多项式，也就是点斜式直线方程。

当n=2时，

f（X）二f（x。

）f[Xo,Xi]（X-X。

）f[Xo,Xi,X2】（X-Xo）（X-Xi）

f[X,Xo,

Xi，X2】（X-Xo）（X-Xi）（X-X2）

N2（x）二f（X。

）f[Xo,Xj（X-X。

）f[Xo,Xi,X2】（X-Xo）（X-Xi）这就是牛顿二次插值多项式。

显然，

N2（x。

"f（x。

）

%（%）=f（X。

）丄^生』（Xi-X。

）=f（Xi）

X。

-％

丄f（x。

）-f（xj

”2（X2）=f（x。

）-丄（X2-X。

）

X。

—Xi

斗丄免S）迪迤L-疋咫Xi）

X）—X2iX。

—XXf丿

二f（x2）

即N2（x）满足二次插值条件。

例2:

已知

f（x）

求满足以上插值条件的牛顿型插值多项式解：

由于：

f（X。

）=0f[Xo,XiP1f[Xo,Xi,X2】=4f[Xo,X!

X2,X3p1.25

则牛顿三次插值多项式为

N3（x）二0（x1）4（x1）（x3）

1.25沁（x1）（x3）（x4）。

例3:

已知f（x）在六个点的函数值如下表，运用牛顿型插值多项式求f（0・596）的近似值。

f（Xk）

一阶差

商

二阶差

商

三阶差

商

四阶差商

五阶差商

X人

0.40

0.41075

0.196

0.55

0.57815

1.1160

0.046

0.65

0.69675

1.1860

0.2800

-0.054

0.80

0.88811

1.2757

0.3588

0.1970

-0.204

0.90

1.02652

1.3841

0.4336

0.2137

0.0344

-0.454

1.05

1.25386

1.5156

0.5260

0.2310

0.0346

0.0003

展开阅读全文