联合态密度和临界点.doc
《联合态密度和临界点.doc》由会员分享,可在线阅读,更多相关《联合态密度和临界点.doc(11页珍藏版)》请在冰点文库上搜索。
3.3联合态密度和临界点
上面我们从微观跃迁过程出发给出了理想晶体由直接跃迁(或竖直跃迁)决定的吸收光谱的一般表达式。
材料吸收光谱的具体形式显然依赖于材料具体的能带结构。
但是,不同材料的光谱存在一个共有的特点:
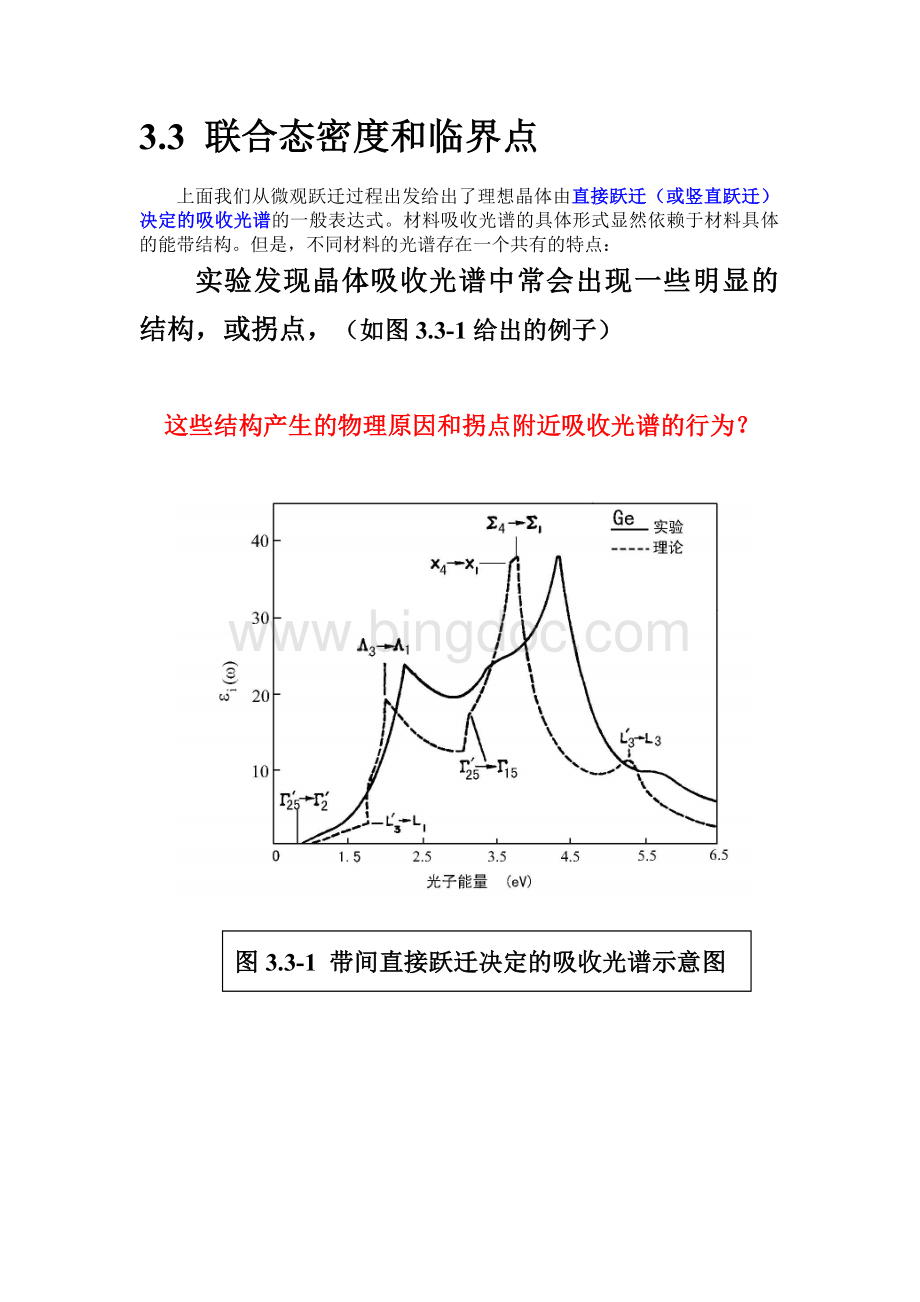
实验发现晶体吸收光谱中常会出现一些明显的结构,或拐点,(如图3.3-1给出的例子)
这些结构产生的物理原因和拐点附近吸收光谱的行为?
图3.3-1带间直接跃迁决定的吸收光谱示意图
3.3.1联合态密度和临界点
(jointorcombineddensityofstates
andcriticalpoint)
考查计算或的公式:
积分的被积函数中的矩阵元除了在一些特殊的值(由于对称性)变为零,一般来说是的平滑函数。
即或中一些拐点,不会是由于矩阵元对的依赖关系。
在这些拐点附近(很小),这矩阵元可近似地看作常数,移出积分号。
这一近似的含义是,在这小的能量范围里,满足能量守恒的每个跃迁元过程都有相同的几率,因而总的跃迁速率与可能的跃迁数目成比例。
式中的积分变为:
,(3.3-1)
----给定光场下,波矢和自旋相同,能量间隔为,分属两个带的状态对(在这里,一个在价带,一个在导带)的数密度,称之为联合态密度。
下面的讨论将显示晶体吸收光谱中出现的拐点正是与这联合态密度相联系的。
为明显看出这一点,我们把空间的积分作一改写。
空间的体积元可表示为
,(3.3-2)
其中为曲面上的面元矢量,为面元大小,为波矢增量,它在面元法线方向的投影为。
利用,也即。
就可表示成:
(3.3-3)
上式中,对积分后变为
(3.3-4)
(对比态密度:
空间中,等能面与之间的状态数/dE,它等于这两个空间等能面所夹的壳层体积与之积/dE:
)
由的这一表达式可见,
积分被积函数可能在某些特定的值,,被积函数发散,出现奇点。
称之为临界点(criticalpoint)。
该点对应的带间能量差称为临界点能量。
在这一能量值,联合态密度呈现一个拐点。
由对称性→可能有多个同类临界点
下面限于讨论单个临界点的情形
由于临界能附近的异常变化是由空间临界点附近的一个小范围内状态对数目随E的变化决定的,这范围以外的区域对积分的贡献是常数,我们可以限于讨论临界点附近区域的贡献。
将在临界点附近展开,取到二次项(由临界点条件,一次项显然为零):
(3.3-5)
其中为临界点处的值(临界点能量),都是沿主轴相对临界点的值,展开式系数的大小由的倒数表示,系数的符号则由来表示,即它们可能的取值为。
按的正或负,临界点可分为四类:
极小值点:
对于它,,
在此奇点取极小值;
鞍点(saddlepoint):
对于它,两个取正,一个取负;
鞍点(saddlepoint):
对于它,一个取正,两个取负;
极大值点:
,在奇点取极大值。
联合态密度在这几种临界点相应的临界点能量附近的行为?
讨论中会利用函数的性质:
,(3.3-6)
其中是方程在区间中的第个根。
以下为方便起见,引进新坐标,其中。
于是:
进而,(3.3-1)式
改写为
(3.3-7)
先讨论点,对这一情形,采用球坐标较方便,这时:
(3.3-8)
上式中的积分可利用前面提到的函数的性质(3.3-6)来计算。
方程仅当时,有一正实数根,而且,
由此我们得到:
(3.3-9)
而在时,方程无根,这时。
对鞍点,用柱坐标较方便。
在平面的极坐标为。
(3.3-10)
先对积分,得
(3.3-11)
当时,方程有两个根,
代入上式,得:
(3.3-12)
上面公式中的常数。
(3.3-12)式中的积分有两种情形。
一种是,则恒有。
考察:
在临界能附近(很小),随的变化。
这时:
可以考察一个适当半径的区域内的积分,只要在这区域内,所作的展开(3.3-5)成立,而且。
因为在整个积分区间(布里渊区)中,半径R的柱体以外的区域里的积分,贡献一个常数项。
于是(3.3-12)变为:
(3.3-13)
其中,常数B与能带的具体结构有关,表示与相比为无穷小量。
的情形,要,就需,因而有:
(3.3-14)
这里也同样的选用了半径R足够大的柱体区域为积分区间。
对鞍点和极大点情形,联合态密度行为的讨论非常类似鞍点和极小点的情形,此处不再赘述。
四种临界点附近,联合态密度的行为都列在图表3.3-1中。
上面的讨论关注的是临界点附近小范围里光吸收的急剧变化规律(拐点),因而吸收光谱表达式(3.2-12)中变化相对缓慢的跃迁矩阵元可以看作常数提到积分号外。
要得到完整的吸收光谱就需要考虑跃迁矩阵元的大小随光子能量(或电子能之差)的变化。
显然,这一矩阵元依赖于具体的能带结构。
人们已经对某些具体材料计算了它们的能带结构和相应的吸收光谱,得到与实验相符的结果。
(见图3.3-1)
表3.1-1三维体系联合态密度在临界点附近的行为
(其中,B是一个与能带结构有关的常数)
临界点
联合态密度
图示
M0点
(极点)
M1点
(鞍点)
M2点
(鞍点)
M3点
(极点)
3.3.2直接带材料的光学吸收边和带隙
绝缘晶体由于禁带的存在,当光子能量小于帶隙时,不能被它吸收。
当光子能量大于或等于帶隙时,吸收过程就变得十分明显。
对直接带材料尤其如此,在这一能量附近吸收系数变化剧烈,可从往长波方向很快降到几个。
这种带间跃迁的吸收强度徒然变化的区域称为吸收边,它涉及的能量范围只有十分之几电子伏。
®测量和研究帶隙的基础。
我们知道,直接带材料的价带极大(顶)与导带极小(底)在空间的同一位置,这正是前面讨论的临界点。
为简单起见,设价带和导带极值附近都是各向同性的,抛物线型结构,即那里载子有效质量为一标量。
它们分别用和表示。
于是,竖直跃迁的能量与波矢的关系为:
(3.3-15)
其中由关系式定义的为约化有效质量,它相当于上一小节3.3.1中的。
这时联合态密度为
(3.3-16)
为计算吸收系数或,还要计算矩阵元
(3.3-17)
光的波矢,相应的波矢差不多相同,,但属于不同的能带,几乎正交,因而上式中第二项的值很小。
因而
当不为零,也即为允许跃迁时,第二项比第一项小得多,于是
(3.3-18)
而当为零,跃迁禁戒时,跃迁速率则由第二项决定。
于是
(3.3-19)
上式利用了(3.3-15)式
以上两式常用来从实验上判断跃迁是允许的还是禁戒的,并由实验确定帶隙的大小。
(由关系式又可得)