高等数学第五章定积分总结Word文档格式.docx
《高等数学第五章定积分总结Word文档格式.docx》由会员分享,可在线阅读,更多相关《高等数学第五章定积分总结Word文档格式.docx(29页珍藏版)》请在冰点文库上搜索。
b]上连续,则f(x)在[a,b]上可积.
1
例1.求xdx
解:
f(x)x在[0,1]连续,积分存在.
1n
0xdxlim0i1ixi与[0,1]的分割法和
的取法无关
.选取特殊的分割法和取点法
可使计算简便.
(1)
将[0,1]n
等分,
ixi
取点i=
ixi,
f(i)
xi
ni2n
(3)
求和f(i)
i1
i
2
1n(n
1)
(4)
取极限limf(
11
xdx
02
i)
lim
n(n1)
2n2
3.
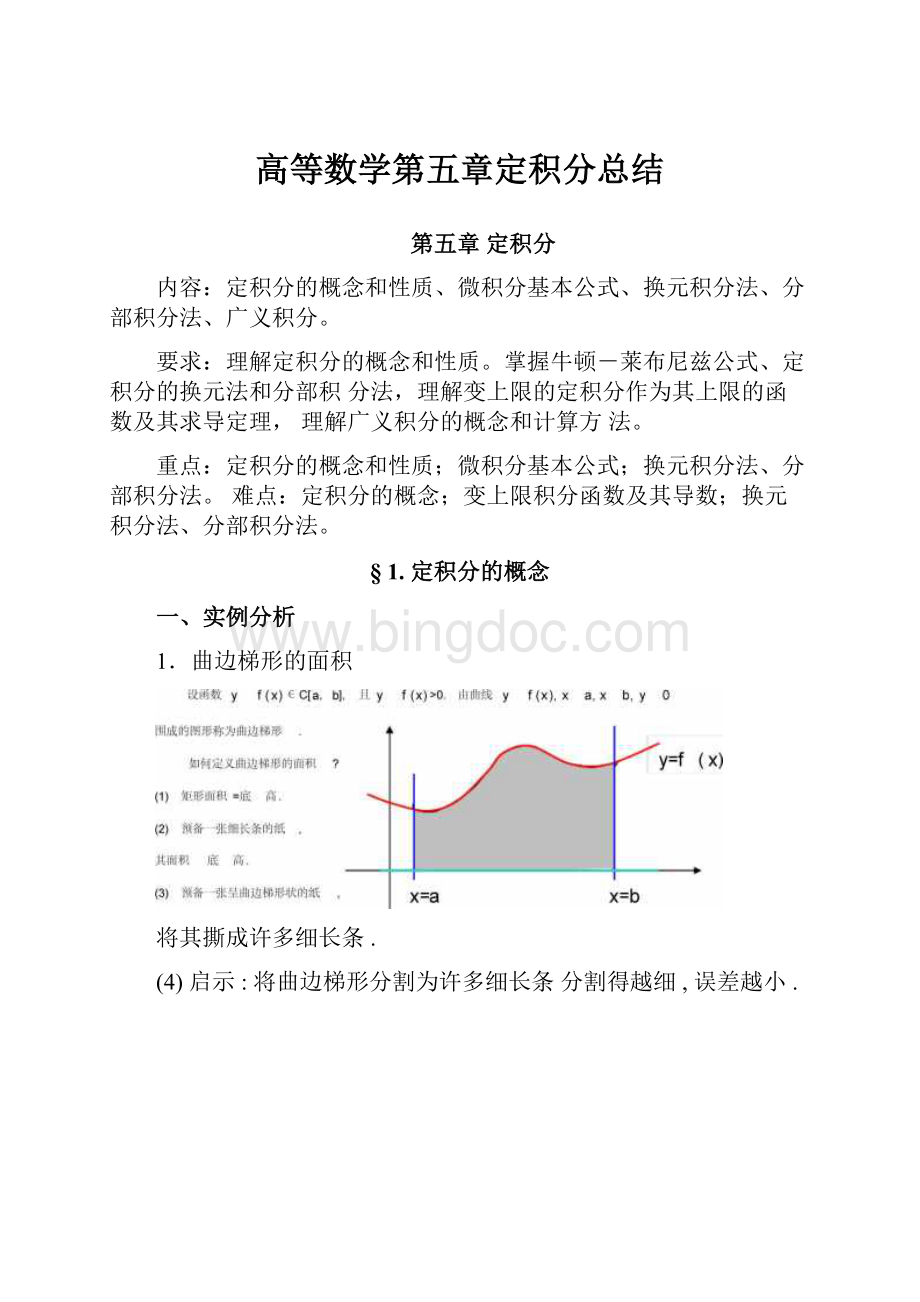
定积分的几何意义
若f(x)在[a,
则af(x)dx=曲边梯形面积;
b]上非负,
f(x)dx的几何意义是由曲线a
f(x),xa,xb,y0围成曲边梯形面积的代
数和.
三、定积分的性质
1.规定
a
(1)f(x)dx0a
f(x)dx
(2)af(x)dx
2.性质
akf(x)
kf(x)dxa
a[f(x)
g(x)]dx
af(x)dx
c
af(x)
cf(x)dx
g(x)dx
推论1若f(x)g(x)(ab),则f(x)dxa
推论2f(x)dx
(5)设M、m分别为f(x)在[a,b]上的最大、最小值(ab),则
m(ba)f(x)dxM(ba)
(6)(积分中值定理)设f(x)C[a,b],则(a,b),使得
f()(ba)
y=f(ξ)
将中值定理变形得:
f(x)dxba
称为f(x)在[a,b]上的平均值.
2.微积分基本公式
、变速直线运动中的位置函数与速度函数之间的关系(略)
、积分上限的函数及其导数
x
设f(x)在[a,b]上连续,则x[a,b],有f(x)在[a,x]上连续.从而f(x)dx存
在.
在这里,积分上限x与被积变量x的性质是不同的.f(x)dx与a、b、f有关,与x
无关.
xx
f(x)dxf(t)dt与a、x、f有关.aa
记作(x),即:
称为积分上限的函数.
定理若f(x)在[a,b]上连续,则积分上限的函数
在[a,b]上可导,且
f(x)在[a,b]上不连续,则最后一个等式不成立.
此定理说明,(x)f(t)dt是f(x)的一个原函数.
例1.
x22sint2dtsinx2
例2.
G(x)0xetdt,求G(x)
xt
etdt
例3.求极限lim0
x0sinx
三、牛顿—莱布尼茨公式
定理若f(x)在[a,b]上连续,F(x)是f(x)的一个原函数,则
af(x)dx
F(b)F(a)
证明:
F(x)是f(x)的一个原函数,
(x)f(t)dt也是f(x)的一个原函数,同a
一个函数的两个原函数之间相关一个常数
于是有:
f(t)dtF(x)
F(x)C
f(x)dx
F(b)
F(a)
f(x)dxF(b)
1.
2.
4x(1
x)
dx
记作
F(x)
记作ba
4x(1x)
1dx
2dx12
1x
2arcsinx12
2(412)3
lnx
ln2
例4.
2xdx
3
2xdx
22(x)dx
2xdx
20
x2
22例5.maxx,xdx0
18
23
22122
0maxx,x2dx0xdx0x2dx
例6.sinxsinxdx
sinxsin3xdx
0sinxcosxdx
02sinxcosxdx
sinx(cosx)dx
sinx2
注:
在数学计算过程中,要对结论(答案)作合理性检验
3.定积分的换元法和分部积分法
、定积分的换元法
则:
f(x)dxf[(t)](t)dt.
定理若f(x)C[a,b],x(t)满足如下条件:
(t)是[α,
β](或[β,α])上单值单调函数
(t)在[α,
β](或[β,α])有连续导数;
()a,
()b
4x2例1.x02x
与不定积分换元法相比较,有两点不同:
(1)积分变量由x变为t时,积分的上下限也要随之改变
(2)求出关于t的原函数后无须回代成x的函数.
21
2xx2
xsect
1cost
34sect
23secttant
dt
24
(1)dt
12
换元积分公式,满足(t)所要求的条件很重要,如
t111
2dx1
(2)dtx11t
1t2
111t2dtI
而事实上,
arctanx112,其原因在于
(t)在t=0不可导.
例3.
证明:
(1)若f(x)是[-a,a]上的偶函数,则
f(x)dxa
0f(x)dx
(2)若证明f(x)是[-
a,a]上的奇函数,则
f(x)dx0a
f(x)dx
0f(x)dx
0x
t0
af(
0f(x)dx0f(x)dx0[f(x)
t)d(t)
0f(t)dt
0f(
x)dx
f(x)]dt
此例提示我们
在计算定积分时,看到对称的积分限
要保持敏感.
例1cos4x(
35
x3x5)0.
例4.f(x)C[0,1],证明:
(1)2f(sinx)dx2f(cosx)dx
(2)xf(sinx)dxf(sinx)dx
xsinx
并计算2dx
01cos2x
(1)2f(sinx)dx
(2)xf(sinx)dx
f(cost)d(t)2f(cosx)dx20
(t)f(sint)d(t)
f(sinx)dxtf(sint)dt
2xf(sinx)dx
f(sinx)dx
2dx
01cos2x2
sinx
1cosx
2dcosx
arctan(cosx)0
arctan(cosx)
、定积分的分部积分法
uvdxudvuvvduuvvudx
uvdxa
bbb
udvuvbavudx
aa
定积分的分部积分法适用的函数类型与不定积分的分部积分法相同
xexdx
lndx3ln32ln212
In
2n
2cos
xdx(nN)
02cos
nxdx
02cosn1xdsinx
n12
cosxsinx02
02sinxdcosn1x
(n
22
2sinxcos
2xdx(n1)
02(1cos2x)cosn
02[cosn2x
1)(In2
In)
nIn(n
1)In2
n1In
(n1)(n
I0
I1
cos
x]dx
3)31
n(n2)42
(n1)(n3)42I
n(n2)531
2cosx0dx
2cosxdx
(n1)(n3)42
n(n2)53
n1In2n2n3In4n4
2n4
n为偶数
n为奇数
(n1)!
!
n为偶数
积分公式:
2sinnxdx2cosnxdxn!
2
n!
00(n1)!
1n为奇数
4.反常积分(广义积分)
定义定积分f(x)dx需满足如下条件:
(1)f(x)有界
(2)f(x)只有有限个间断a
点(3)a,b为确定的数值,即积分限是有限值.反常积分是对无穷积分限和无界函数定
义的积分.
、无穷限的反常积分
定义设f(x)C[a,),取t>
a,若极限
t
tlimaf(x)dx
记作f(x)dx,即:
存在,则称此极限为f(x)在[a,)上的反常积分
类似地,定义:
f(x)dxlim
f(x)dxf(x)dx
tf(x)dx(f(x)C(
b])
f(x)dx(f(x)C(
))
注:
f(x)dx收敛
f(x)dx,f(x)dx都收敛
F(x)f(x)
f(x)dxF(t)F(a)
F(x)f(x)记作
f(x)dxlimF(t)F(a)F(x)a
1.1
01x
2.xexdx
2dxarctanx
0xxexdxlimt
0xlimxdexttlimtett
0xxexdxt
lim[t
lime0
t例3.x2dx
1x2
xxe
texdx]
1xx2dx
x2dx
01xx2dx
12ln(1x2)
(发散)
故1xx2dx发散.
取b>
t>
、无界函数的反常积分
定义设f(x)C(a,b],limf(x)xa
af(x)dx,即:
tlimatf(x)dx
存在,则称此极限为f(x)在(a,b]上的反常积分,仍记作
f(x)dxlimf(x)dx
bb亦称为f(x)dx收敛;
否则,称f(x)dx发散.
若f(x)C[a,b),b
定义:
f(x)dx
若f(x)C{[a,c)b
f(b0)tlimf(x)dxtba
)(c,b]},f(c0)或f(c0)
cbaf(x)dxcf(x)dx
fa
(x)dx收敛
accb
f(x)dx,f(x)dx都收敛ac
例4.dx
limx
x11x2
01
例5.
lnxdx
t1
limt
121
tlim0
lnxdxt
xlnx
1xt
例6.
0(1x)2
lim12
x1(1x)2
0(1x)2
1121
2dx2dx
0(1x)21(1x)2
1lim1发散t11x0
21故0(11x)2dx发散.
计算f(x)dx前,首先判断f(x)在[a,b]上是否有无穷点a
定积分小结
、基本概念
1.定积分
2.变上限积分函数
3.广义积分
1)无穷积分限
2)无穷间断点
二、定积分的性质
1.
定积分与被积分字母无关
af(t)dt
af(u)du
af()d
2.
积分限的分割
f(x)cf(x)dx
3.
积分中值定理
f(x)dxf()(ba)a
4.
对称函数在对称区间上的积分
0f(x)为奇函数
2f(x)dxf(x)为偶函数
三、定积分的计算
1.牛——莱公式
2.换元积分法
3.分部积分法
四、积分上限函数求导
(x)af(t)dtf(x)
u(x)a
f(t)dt
f[u(x)]u(x)
例3.dx
2x