多元线性回归分析.docx
《多元线性回归分析.docx》由会员分享,可在线阅读,更多相关《多元线性回归分析.docx(66页珍藏版)》请在冰点文库上搜索。
多元线性回归分析
多元线性回归分析
直线回归概念复习
例:
为了研究3岁至8岁男孩身高与年龄的规律,在某地区在3岁至8岁男孩中随机抽样,共分6个年龄层抽样:
3岁,4岁,…,8岁,每个层抽10个男孩,共抽60个男孩。
资料如下:
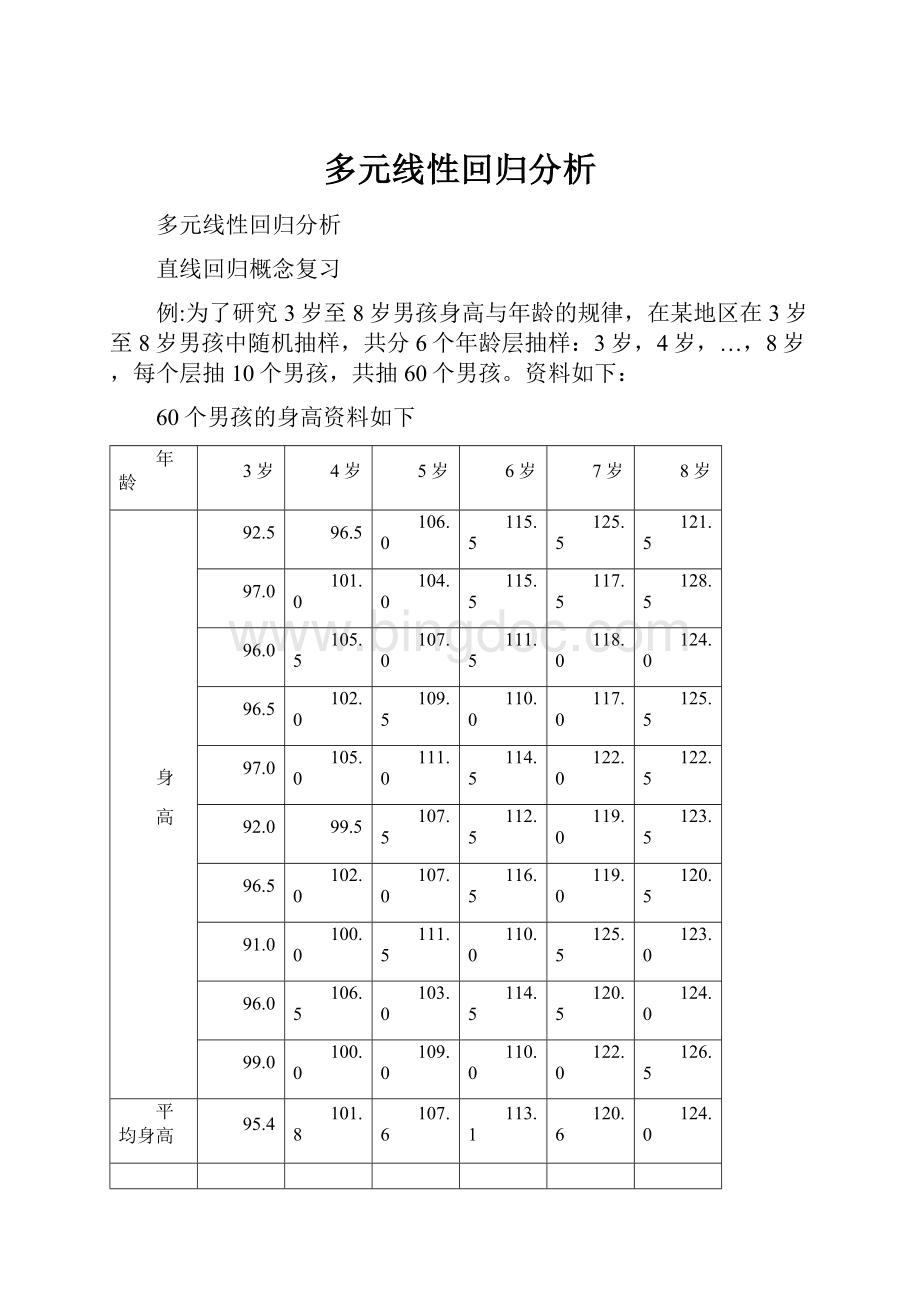
60个男孩的身高资料如下
年龄
3岁
4岁
5岁
6岁
7岁
8岁
身
高
92.5
96.5
106.0
115.5
125.5
121.5
97.0
101.0
104.0
115.5
117.5
128.5
96.0
105.5
107.0
111.5
118.0
124.0
96.5
102.0
109.5
110.0
117.0
125.5
97.0
105.0
111.0
114.5
122.0
122.5
92.0
99.5
107.5
112.5
119.0
123.5
96.5
102.0
107.0
116.5
119.0
120.5
91.0
100.0
111.5
110.0
125.5
123.0
96.0
106.5
103.0
114.5
120.5
124.0
99.0
100.0
109.0
110.0
122.0
126.5
平均身高
95.4
101.8
107.6
113.1
120.6
124.0
从散点图上,我们可以发现样本点(X,Y)随机地出现在一条直线附近,并且从资料背景上考察,同一年龄的儿童身高应近似服从一个正态分布,而儿童身高的总体均数应随着年龄增长而增大,并由每个年龄的身高样本均数与儿童年龄的散点图可以发现:
这些点非常接近一条直线以及样本均数存在抽样误差,因此推测儿童身高的总体均数与年龄可能呈直线关系。
故假定身高Y在年龄X点上的总体均数
与X呈直线关系。
其中y表示身高,x表示年龄。
由于身高的总体均数与年龄有关,所以更准确地标记应为
表示在固定年龄情况下的身高总体均数。
身高的样本均数与年龄的散点图
故有理由认为身高的总体均数与年龄的关系可能是一条直线关系
上述公式称为直线回归方程。
其中为回归系数(regressioncoefficient),或称为斜率(slope);称为常数项(constant),或称为截距(intercept)。
回归系数表示x变化一个单位y平均变化个单位。
当x和y都是随机的,x、y间呈正相关时>0,x、y间呈负相关时<0,x、y间独立时=0。
一般情况而言,参数和是未知的。
对于本例而言,不同民族和不同地区,和往往是不同的,因此需要进行估计的。
由于不同年龄的身高实际观察值应在对应的身高总体均数附近(即:
实际观察值与总体均数之间仅存在个体变异的差异),故可以用年龄和实际身高观察值的资料对未知参数和进行估计,一般采用最小二乘法进行参数估计。
我们将借助Stata软件对本例资料进行直线回归。
数据格式
x
y
3
92.5
3
97.0
3
96.0
3
96.5
3
97.0
3
92.0
3
96.5
3
91.0
3
96.0
3
99.0
4
96.5
4
101.0
4
105.5
4
102.0
4
105.0
4
99.5
4
102.0
4
100.0
4
106.5
4
100.0
5
106.0
5
104.0
5
107.0
5
109.5
5
111.0
5
107.5
5
107.0
5
111.5
5
103.0
5
109.0
6
115.5
6
115.5
6
111.5
6
110.0
6
114.5
6
112.5
6
116.5
6
110.0
6
114.5
6
110.0
7
125.5
7
117.5
7
118.0
7
117.0
7
122.0
7
119.0
7
119.0
7
125.5
7
120.5
7
122.0
8
121.5
8
128.5
8
124.0
8
125.5
8
122.5
8
123.5
8
120.5
8
123.0
8
124.0
8
126.5
回归命令
regressyx
Source|SSdfMSNumberofobs=60
-------------+------------------------------F(1,58)=777.41
Model|5997.7157115997.71571Prob>F=0.0000
Residual|447.467619587.71495895R-squared=0.9306
-------------+------------------------------AdjR-squared=0.9294
Total|6445.1833359109.240395RootMSE=2.7776
------------------------------------------------------------------------------
y|Coef.Std.Err.tP>|t|[95%Conf.Interval]
-------------+----------------------------------------------------------------
x|5.854286.209965427.880.0005.4339946.274577
_cons|78.184761.20920264.660.00075.7642880.60524
------------------------------------------------------------------------------
回归方程
b=5.854286,a=78.18476
se(b)=0.2099654
回归系数检验:
H0:
=0vsH1:
0
回归系数统计量t=b/se(b)=5.854286/.2099654=27.88,P值<0.001,
95%CIof为(5.433994,6.274577)
1)简述单因素线性回归方程y=+x在实际分析中要注意的问题
(a)残差i=yi-a-bxi,引入回归模型yi=+xi+i
(b)i~N(0,)且{i}相互独立:
说明有三个条件:
i)i服从正态分布
ii){i}相同的方差2。
iii){i}相互独立。
(c)不满足上述3个条件时,反映在实际回归分析时,有如下情况:
i)散点在直线一侧较多而且靠直线很近,当在直线的另一侧,散点较少,而且离直线较远,反映在误差项偏态分布。
ii)散点随着自变量x增大而离散程度增大或减小(喇叭口状),反映了误差项方差随着x变而变,即不满足相同方差(方差齐性)。
iii)随着xi变化而i呈某种规律性的变化。
反映还含有x的信息未利用到,还可以继续改进回归模型。
问题1:
在同一总体中随机抽取2个相同样本量的样本,每个样本中都含有变量x和y,并以y为因变量和x为自变量,作线性回归,请问:
两个样本作出的回归方程一样吗?
它们之间什么关系?
问题2:
回归方程所示的直线与原始数据的关系是什么?
1)不同,它们之间存在抽样误差
2)回归分析统计背景:
对于固定自变量x,对y所在的总体进行抽样,得到在固定x情况下,y的样本值,因此对于每个xi,得到对应的抽样值yi。
即:
资料为:
(x1,y1),(x2,y2),…,(xn,yn)。
因此对于同一个x值,y所对应的总体均数
相同,不同的x值,y所对应的总体均数
可能不同。
如果y的总体均数值
与x的关系呈直线关系
,则样本资料(x1,y1),(x2,y2),…,(xn,yn)呈带状直线散点图。
由于抽样资料y=总体均数
+抽样误差
因此如果y的总体均数值
与x呈直线关系
,则抽样资料
当
,则对于固定x,
,而用样本资料(x1,y1),(x2,y2),…,(xn,yn)所估计得到的回归方程
是固定x情况下,y的总体均数与x的线性方程的表达式
。
即:
b是β的样本估计值(无偏估计),a是α的样本估计值(无偏估计),
是
的样本估计值。
抽样误差(估计值)=样本资料-(a+bx)(即:
的估计值:
残差)
所以要求回归分析的资料,其残差服从正态分布,且与x无关、方差齐性。
2)引入多元线性回归模型定义
(a)例3-1,研究女中学生的肺活量与体重和胸围的关系,随机抽样了10名女中学生的体重x1(kg),胸围x2(cm)和肺活量y(ml),资料如表3-1,试建立一个因变量为y对自变量x1,x2的线性回归方程。
(b)对于相同的体重x1和胸围x2,考查女中学生的肺活量y总是有一定的变异的,但总对应有一个总体均数y|X,而且总体均数y|X可能与体重x1和胸围x2有关。
x1和x2与总体均数y|X最简单的关系为线性关系:
i)同样的x1和x2,观察值y与总体均数y总有一定的随机误差,即y-y|X=,因此
ii)若~N(0,2)分布且独立,而观察值
,则称肺活量y、体重x1和胸围x2符合线性回归模型
(c)对于一般的线性回归模型定义为:
i)设有p个观察自变量x1,x2,…,xp,并用向量
X=(x1,x2,…,xp)’,因变量为y,且记y的总体均数为
,随机误差~N(0,2)且独立,则线性回归模型可以表示为
对于观察值(y1,X1),(y2,X2),…,(yn,Xn),其中Xi=(xi1,xi2,…,xip),i=1,2,…,n。
对应的线性回归模型为
且独立。
在本例中,作线性回归如下:
(介绍一下数据结构)
.regressyx1x2
Source
SS
df
MS
Numberofobs=10
F(2,7)=6.75
回归平方和
回归均方和
Model
1895106.55
2
947553.275
Prob>F=0.0232
残差平方和
残差均方和
决定系数
Residual
982143.45
7
140306.207
R-squared=0.6587
校正和决定系数
AdjR-squared=0.5611
Total
2877250.00
9
319694.444
RootMSE=374.57
总平方和SS总描述样本量为n=10的因变量y总的变异。
回归平方和SSR描述了样本量为n时,由自变量x1,x2变化而引起的因变量y的这部分变异,SSe描述了样本量为n时,由随机误差项所引起的因变量y的一部分变异,因此:
总变异=自变量引起y的变异+随机误差引起变异
对应:
SS总=SS回归+SS误差
由于SS总,SS回归和SS误差均与样本量n有关,样本量n越大,对应变异就越大。
所以取平均变异指标:
均方差MS
,
回归系数
回归系数标准误
t值
P值
95%可信区间
y
Coef.
Std.Err.
t
P>|t|
[95%Conf.Interval]
x1
113.9987
38.31109
2.976
0.021
23.40741
204.5901
x2
45.48368
28.18428
1.614
0.151
-21.16155
112.1289
_cons
-5545.806
2293.933
-2.418
0.046
-10970.1
-121.5156
回归方程
解释回归系数的意义
简述SST总=SSR回归+SSE残差,
自由度df回归=模型中的回归系数个数(不含常数项),df残差=n-df回归-1
,
模型的假设检验H0:
1=2=0vs1,2不全为0
当H0成立时,
~F(df回归,df残差)
单个回归系数检验:
H0:
=0vsH1:
0
当H0:
=0成立时,
简述回归系数的95%CI意义与t检验的对应关系。
(d)假设检验一般情况叙述
(e)决定系数
(f)复相关系数R
(g)H0:
1=2=…=r=0vs1,2,…,r不全为0。
当H0成立时
(x1,x2,…,xp)的估计及其误差
(STATA命令:
predicty1)
(STATA命令:
predictmeansd,stdp)(因为
有抽样误差)
95%CI
,自由度v=n-1-p
个体预测值和标准误
(STATA命令:
predicty1)
线性回归模型应用的条件总结
理论上
且独立。
具体检查是否复合线性回归模型步骤
1.先做线性回归
2.计算残差i
3.检查残差i是否服从正态分布(引起正态分布)
4.检查残差i的离散程度是否与其它自变量呈某种趋势关系。
(要求无任何趋势关系)
5.检查残差i变化是否与其它自变量呈某种对应趋势关系。
(要求无任何趋势关系)
多元线性回归常见的应用以及应用中的问题
●全回归模型(析因分析)
●多重共线对分析的影响VIFs(varianceinflationfactors)
●对于自变量p个自变量x1,x2,…,xp中,以其中一个xi作为因变量作回归以及其它p-1个变量为自变量,得到相应的决定系数Ri。
定义xi的膨胀因子
●VIFi=1对应
说明xi与其它p-1个自变量无共线。
●当
对应VIFi>1
●当
,说明xi与其它p-1个自变量完全共线,对应VIFi成为无穷大。
●通常认为在p个自变量x1,x2,…,xp中,最大的VIF>10,则认为严重共线,最小二乘估计受到较严重的影响。
●平均VIF=
>>1,则认为
●寻找影响因变量的主要因素。
●用回归进行两组或多组的均数比较并校正混杂因素的影响。
全回归分析举例
例:
据儿童保健部门的考察,4至7岁儿童的身高与年龄近似呈线性关系,且男女身高也有差异。
下列收集了50名男孩和50名女孩的身高,年龄均在4岁至7岁之间。
请试建立回归方程描述年龄与身高的关系(其中sex=1表示男,sex=0表示女)
sex
age
y
1
4.5
90
1
6.5
111
1
6.2
107
1
6.4
107
1
6.7
114
1
4.4
88
1
6.4
109
1
4.2
86
1
6.2
107
1
7.4
122
1
5
95
1
4.1
85
1
5.6
100
1
7.5
121
1
6
106
1
7.3
120
1
4.8
93
1
6.2
105
1
5
94
1
7.7
125
1
5.1
96
1
4.4
88
1
5.6
101
1
6.8
113
1
7.4
121
1
5.8
105
1
5.6
102
1
7.5
122
1
4.2
84
1
6.7
113
1
6.8
115
1
6.7
114
1
4.9
93
1
4.3
86
1
6.3
108
1
5.4
99
1
7.2
116
1
4.4
87
1
6.3
109
1
4.4
89
1
7.8
125
1
4.8
92
1
5
95
1
4.6
90
1
7
117
1
5.4
99
1
5.5
102
1
7.8
127
1
6.3
110
1
7.1
119
0
4.3
87
0
7.2
114
0
5
95
0
5.8
100
0
4.5
90
0
4.9
91
0
4.1
86
0
4.6
90
0
5.1
94
0
6.5
109
0
7.5
116
0
5.9
104
0
4.9
94
0
7.7
118
0
7.5
116
0
7.4
117
0
4.7
91
0
6.5
107
0
6.9
112
0
6.1
105
0
4.3
89
0
5.5
99
0
4.1
85
0
7.2
113
0
5.6
101
0
6
104
0
5.4
98
0
5.1
95
0
5.6
101
0
4.7
90
0
7.9
120
0
4.7
90
0
5.1
95
0
4.9
94
0
6.4
108
0
4.3
88
0
6.2
107
0
6.8
110
0
5
94
0
4.8
94
0
5.9
104
0
6.4
107
0
4.7
93
0
7.4
116
0
6.8
110
0
5.4
99
0
5.4
99
0
5.1
96
0
7.3
115
0
7.8
121
考虑身高总体均数为
模型为:
用拟合上述模型
gensexage=sex*age
regressyagesexsexage
------------------------------------------------------------------------------
y|Coef.Std.Err.tP>|t|[95%Conf.Interval]
-------------+----------------------------------------------------------------
sex|-9.5137941.119899-8.500.000-11.73678-7.290813
age|9.075835.133735467.860.0008.8103729.341298
sexage|1.929241.188310610.240.0001.5554472.303035
_cons|48.97983.786966862.240.00047.4177150.54194
回归方程为
则女孩为身高与年龄的回归方程为(sex=0)
age的回归系数的意义为每年身高增长的速度
则男孩为身高与年龄的回归方程为(sex=1)
age的回归系数的意义为每年身高增长的速度
因此女孩身高的增长速度为2,样本估计值为9.075835
男孩身高的增长数为2+3,样本估计值为11.005076
男孩与女孩身高的增长速度差异为3,3>0说明男孩身高增长速度快,3<0说明女孩身高增长速度快,3说明女孩与男孩的身高增长速度是一样的。
样本估计值为1.929241>0,P值<0.001。
因此男孩身高速度高于女孩,并且差别有统计学意义。
例:
治疗缺铁性贫血100人,随机分为2组,给予不同疗法治疗:
经过一个月治疗后,治疗前后的红细胞数(万/l)如下:
A组
B组
治疗前
y1
治疗后
y2
组别
group
治疗前
y1
治疗后
y2
组别
group
325
337
1
327
348
0
312
325
1
334
354
0
331
343
1
347
368
0
328
341
1
317
337
0
316
330
1
351
371
0
367
380
1
299
319
0
354
367
1
336
357
0
311
325
1
317
338
0
364
378
1
305
326
0
345
360
1
362
382
0
335
348
1
315
333
0
329
344
1
370
394
0
336
349
1
346
368
0
293
306
1
324
345
0
345
358
1
324
346
0
364
378
1
362
383
0
311
325
1
318
338
0
347
360
1
329
350
0
350
364
1
356
378
0
295
308
1
356
376
0
369
383
1
356
378
0
323
336
1
340
362
0
385
399
1
322
342
0
324
338
1
310
330
0
312
325
1
357
378
0
322
336
1
345
365
0
340
353
1
340
361
0
330
344
1
330
351
0
347
361
1
358
380
0
361
374
1
306
329
0
374
389
1
322
342
0
327
340
1
304
325
0
335
349
1
327
348
0
363
377
1
353
374
0
338
350
1
355
376
0
328
344
1
346
369
0
303
316
1
369
390
0
329
342
1
326
348
0
317
331
1
333
355
0
334
346
1
367
389
0
334
348
1
363
384
0
335
348
1
337
360
0
330
343
1
368
389
0
338
353
1
339
361
0
353
366
1
337
358
0
332
345
1
369
390
0
303
317
1
358
380
0
369
384
1
357
378
0
328
343
1
345
368
0
治疗前
治疗后
第一组
335.2820.840541
348.8221.04678
第二组
339.9819.875623
361.1420.188914
考虑以治疗前后的改变量为评价的效应指标
先不考虑校正基线
则可以用成组t检验进行统计分析
geny=y2-y1
ttesty,by(gro