数学论文 证明三角形内角和等于180度Word格式文档下载.docx

数学论文 证明三角形内角和等于180度Word格式文档下载.docx

《数学论文 证明三角形内角和等于180度Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《数学论文 证明三角形内角和等于180度Word格式文档下载.docx（10页珍藏版）》请在冰点文库上搜索。

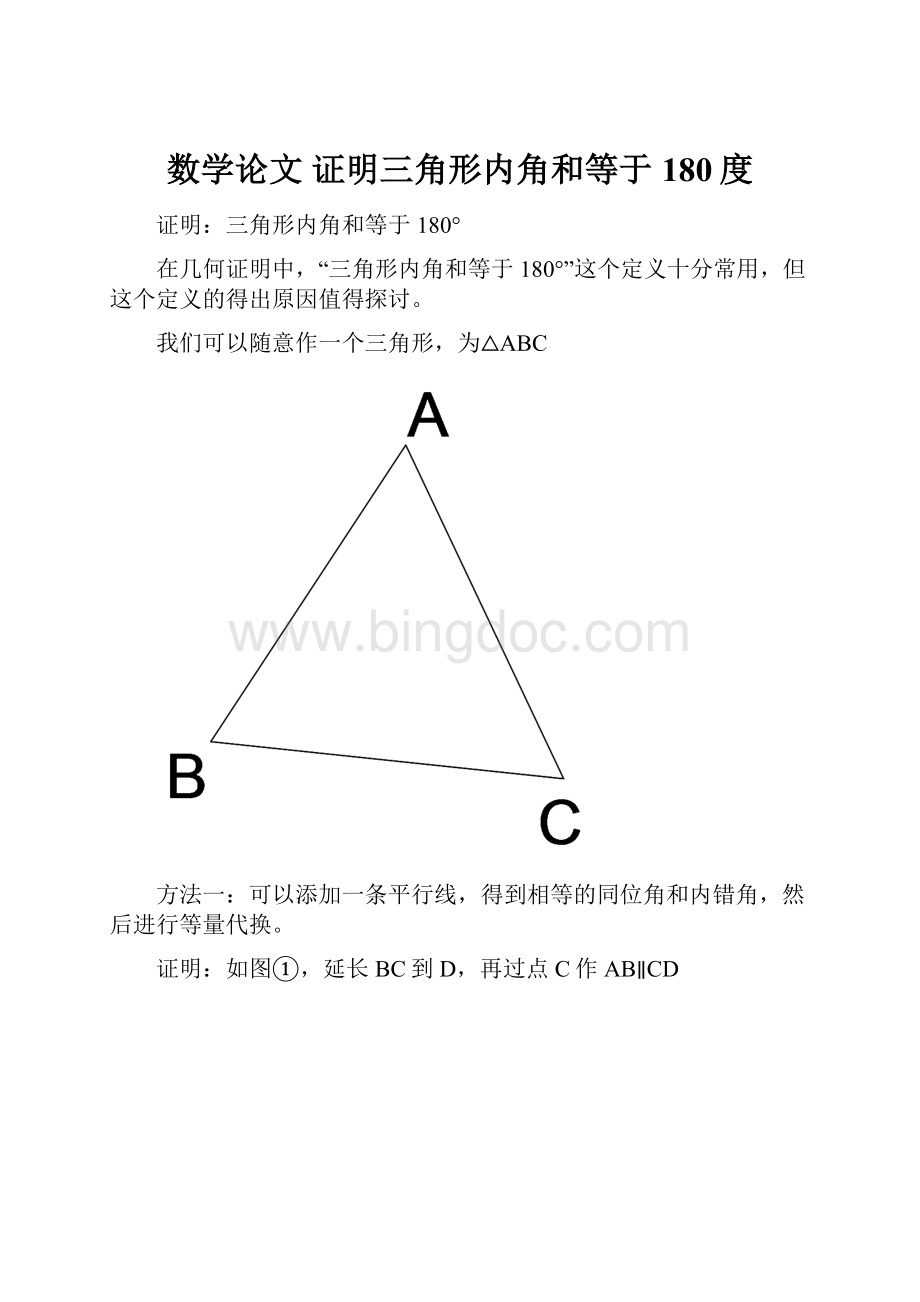
∵AB∥CD（已知）

∴∠B＝∠ECD（两直线平行，同位角相等）

∠A＝∠ACE（两直线平行，内错角相等）

∵∠ACB＋∠ECD＋∠ACE＝180°

（平角为180°

）

∴∠ACB＋∠B＋∠A＝180°

（等量代换）

方法二：

证明：

如图②，过点A作AD∥BC

∵AD∥BC

∴∠DAC＝∠ACB

∠EAB＝∠ABC

∵∠EAB＋∠BAC＋∠DAC＝180°

∴∠ABC＋∠BAC＋∠ACB＝180°

方法三：

如图③，过点A作AD∥BC

∵AD∥BC 

∴∠C=∠DAC（两直线平行，内错角相等） 

∠DAB+∠B=180°

（两直线平行，同旁内角互补） 

∵∠DAB=∠DAC+∠CAB 

∴∠DAC+∠CAB+∠B=180°

∵∠C=∠DAC 

∴∠C+∠CAB+∠B=180°

方法四：

如图④，过A点作DE∥BC，延长BA、CA交DE于A点

∵DE∥BC

∴∠C=∠FAD

∠B=∠GAE（两直线平行，同位角相等）

∵D,A,E三点共线

∴∠DAE=180°

∵∠DAE=∠DAF+∠FAG+∠GAE

∴∠DAF+∠FAG+∠GAE=180°

∵∠GAF=∠BAC（对顶角相等）

∴∠BAC+∠C+∠B=180°

方法五：

如图⑤，作直线DE∥AC，FE∥AB交BC于E

E

∵DE∥AC 

∴∠AFE+∠DEF=180°

∠C=∠DEB（两直线平行，同位角相等） 

∵FE∥AB 

∴∠AFE+∠A=180°

∠B=∠FEC（两直线平行，同位角相等） 

∴∠A=∠DEF 

∵B,C,E三点共线 

∴∠BEC=180°

∵∠BEC=∠DEB+∠DEF+∠FEC 

∴∠DEB+∠DEF+∠FEC 

=180°

∴∠A+∠C+∠B=180°

方法六：

如图⑥，作DE∥AC，FG∥AB，MN∥BC，都交于点O

∵DE∥AC

∴∠AFO+∠FOD=180°

（两直线平行，同旁内角互补）

∵FG∥AB

∴∠AFO+∠A=180°

（两直线平行，同旁内角互补）∴∠A=∠FOD

∵MN∥BC

∴∠C=∠FNO（两直线平行，同位角相等）

∴∠FNO=∠DOM（两直线平行，同位角相等）

∴∠C=∠DOM

∴∠B=∠DMO（两直线平行，同位角相等）

∴∠DMO=∠FON（两直线平行，同位角相等）

∴∠B=∠FNO

∵M,O,N三点共线

∴∠MON=180°

∵∠MON=∠DOM+∠DOF+∠FON

∴∠DOF+∠DOM+∠FON=180°

∴∠A+∠B+∠C=180°

方法七：

如图⑦，作DE∥AC，FG∥AB，MN∥BC，都交于点O 

延长AC交FG于点K，延长AB到点L，延长BC交FG于点P

∵ 

MN∥BC 

∴∠ABC=∠AHN

∠ACB=∠ANM（两直线平行，同位角相等） 

∵ 

AB∥FG 

∴∠AHN=∠FON

∠BAC=∠AKO 

（两直线平行，同位角相等） 

∴∠ABC=∠FON 

DE∥AC 

∴∠ANM=∠DOM 

∠OKA=∠DOF 

（两直线平行，内错角相等） 

∴∠ACB=∠DOM 

FG∥AB 

∴∠BAC=∠OKA（两直线平行，同位角相等） 

∴∠BAC=∠DOF 

M,O,N三点共线 

∵∠MON=∠DOM+∠DOF+∠FON 

∴∠DOM+∠DOF+∠FON=180°

∴∠BAC+∠CBA+∠ACB=180°