多元函数微分学讲义doc.docx
《多元函数微分学讲义doc.docx》由会员分享,可在线阅读,更多相关《多元函数微分学讲义doc.docx(29页珍藏版)》请在冰点文库上搜索。
多元函数微分学讲义doc
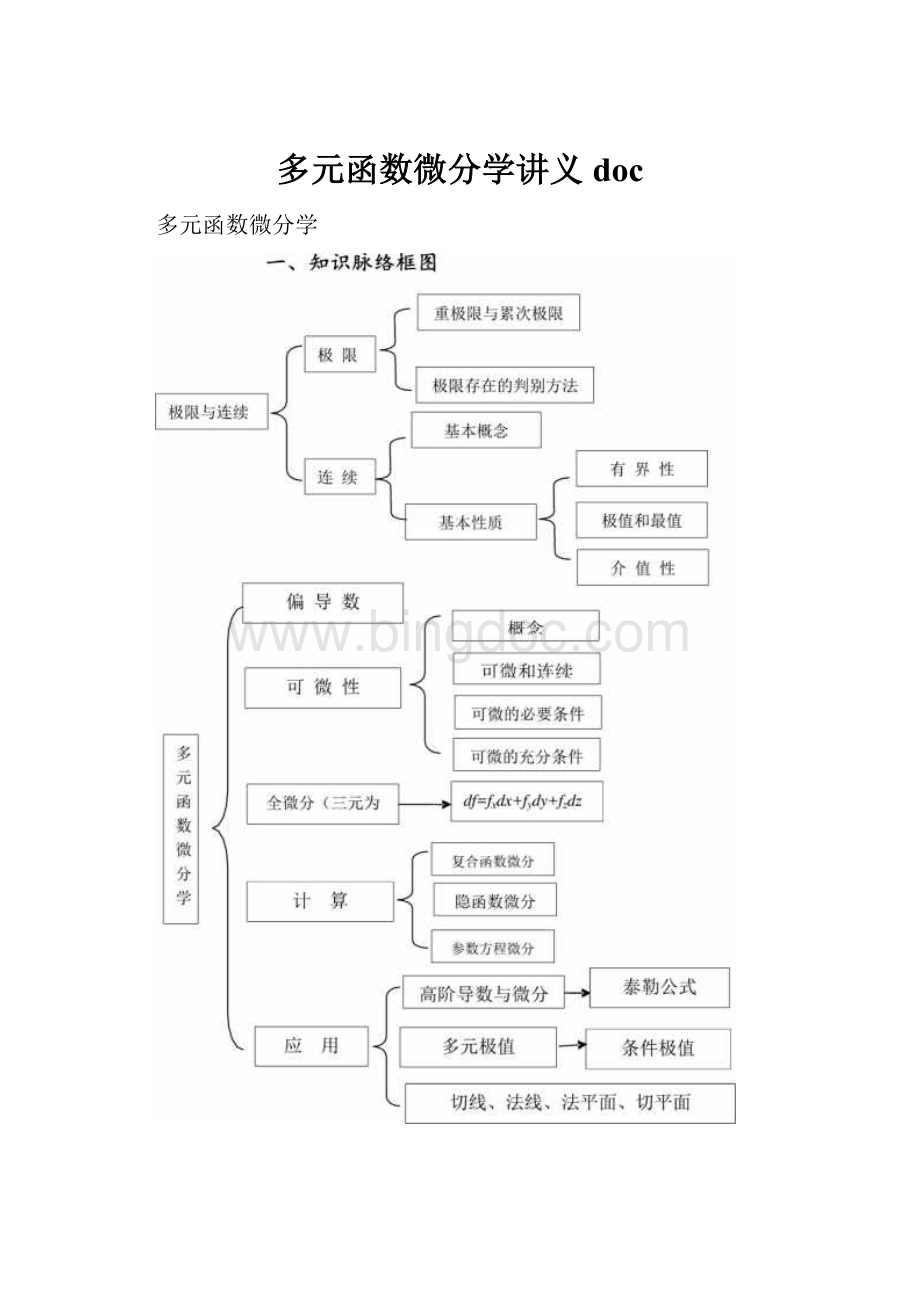
多元函数微分学
二、本章重点及难点
本章需要重点掌握以下几个方面内容:
•偏导数、全微分及其儿何意义,可微与偏导存在、连续之间的关系,复合函数的偏导数与全微分,一阶微分形式不变性,方向导数与梯度,高阶偏导数,混合偏导数与顺序无关性,二元函数中值定理与Taylor公式.
•隐函数存在定理、隐函数组存在定理、隐函数(组)求导方法、反函数组与坐标变换.
•几何应用(平面曲线的切线与法线、空间曲线的切线与法平面、曲面的切平面与法线.
•极值问题(必要条件与充分条件),条件极值与Lagrange乘数法.
三、本章的基本知识要点
(一)平面点集与多元函数
1.任意一点A与任意点集E的关系.
1)内点.若存在点A的某邻域U(A),使得U(A)uE,则称点A是点集E的内点。
2)外点.若存在点A的某邻域"(A),使得U(A)cE=0,则称点A是点集E的
外点。
3)界点(边界点)・若在点A的任何邻域内既含有属于E得的点,又含有不属于£的点,则称点A是点集E的界点。
4)聚点.若在点A的任何空心邻域U°(A)内部都含有E中的点,则称点A是点集E
的聚点。
5)孤立点.若点AeE,但不是E的聚点,则称点人是点集E的孤立点。
2.儿种特殊的平面点集.
1)开集.若平面点集E所属的每一点都是E的内点,则称E为开集。
2)闭集.若平面点集E的所有聚点都属于则称E为闭集。
3)开域.若非空开集E具有连通性,即E中任意两点之间都可用一条完全含于E得有限折线相连接,则称E为开域。
4)闭域.开域连同其边界所成的点集称为闭域。
5)区域.开域、闭域或者开域连同某一部分界点所成的点集,统称为区域。
3.A?
上的完备性定理.
1)点列收敛定义:
设{4}uR2为平面点列,%R2为一固定点。
若对任给的正数
存在正整数N,使得当n>N时,有乙6(/(气,功,则称点列{4}收敛于点玲,记作
lim—*或4-*,(〃—8).
以T8
2)点列收敛定理(柯西准则)平面点列{4}收敛的充要条件是:
任给正数存在正整数N,使得当n>N时,对一切自然数知都有”(4,4+a)ve.
3)闭区域定理.设{£>〃}是A?
中的闭域列,它满足:
⑴Ogi,〃=l,2,...;(ii)=d(D)limd〃=0.
〃一>8
则存在唯一的点疑以=1,2,....
4)聚点定理.设EUR?
为有界无限点集,则E在A?
中至少有一个聚点。
5)有限覆盖定理.设DuV为一有界闭域,{△“}为一开域族,它覆盖了。
(即
Dup&),则在{△*中必存在有限个开域△”△2,它们同样覆盖了。
(即m
Du)oj=l"
4.二元函数
定义:
设平面点集DuR2,若按照某对应法则f,。
中每一点P(x,y)都有唯一确定的
实数z与之对应,则称/'为定义在。
上的二元函数(或称/为。
到R的一个映射),记作
f.D—R,
P—z,
且称。
为/的定义域,PwD所对应的z为f在点P的函数值,记作z=f(P)或
Z=f(x,y)。
(注:
其它多元函数与二元函数相似)。
(-)二元函数的极限。
1.定义设/为定义在DuR?
上的二元函数,n为。
的一个聚点,A是一个确定的实数,若对V£>0,都存在一个3〉0,使得PW(哭)c。
时,都有
则称/'在。
上当Pt耳时,以A为极限,记作lim/(P)=A。
有时简记为Pt片)
网质“。
当P、£分别用3y),(x(),y())表示时,上式也可写作limf(x,y)=A.
(.F)t(.",o)
2.重要定理及推论.
1)lim/(P)=A的充要条件:
对于。
的任一子集E,只要藉是E的聚点就有Pt%
性。
g(P)“。
尸一>4)
PeE
2)
3)
设E[UD,丛是耳的聚点,若lim/(P)不存在,则lim/(P)也不存在。
Pt命Pt%
PeD
设耳、E’uD,气是它们的聚点。
若limf(P)=A,lim/(P)=A2,但Af,
PT%P—6
作E]PeE2
则limf(P)不存在。
4)
Pt%
代。
极限lim/(P)存在的充要条件是:
对于。
中任一满足条件的点列{乙},它所P—%
ND
对应的函数列(/(P,)}都收敛。
3.二元函数函数极限的四则运算.
若lim/(X,y)=A,limg(x,y)=B。
贝U
(ETbo)'7(ETwo)'7
1)期[/(3)±g(U)]=A±B;2)既f(x,y)g(矽)=A.8;
3)lim=£(眼0).
(x,),)T(*),},(>)g(x,y)B
4.累次极限.
1)定义:
对于函数f(x,y),若固定y工yo,limf(x,y)=gy)存在,且limp(y)=A
X—>工0)’T)‘O
也存在,则称A为f(x,y)在)处先对*后对y的累次极限,记为limlim/(x,y),类似可定义limlim/(尤,y)。
)f0H(>0
2)重要定理及推论.
%1若limf(x9y}与limlimf(x,y)(或limlimf(x,y})都存在,则它们
(x,y)T(.s),o)XT*y-*>by-^y0刀—命
相等;
%1若lim/(x,y),limlimf(x,y}和limlimf(x,y}都存在,则三者相等;
(X,)')T(%,)'O)XT%yT〉'oXT*
%1若limlimfix,y)与limlimf(x,y)都存在但不相等,贝Ulim/(x,y)不
XTX(>y-»y0>'-*>0XT心(x,y)T(吟,)'O)
存在。
(%1)二元函数的连续性
1.定义设f为定义在点集DuR2上的二元函数,也D,若对Vr>0,都存在一个
3>0,只要PcU(E),$)c。
,就有
则称r关于集合。
在点4连续。
若f在。
上任何点都连续,则称f为D上的连续函数。
若lim[/'3o,),)-f(%yo)]=°,则称在4)=(尤0,允)处关于>连续。
同理可定义关于工连续。
2.复合函数的连续性定理设二元函数u=(p(x,y)和口="(工,);)在Ad%%)点连续,函数z=/(w,v)在点(以o,u°)处连续,其中^(x0,y0),v0=^(x0,y0),则复合函数z=f(仞(x,y),j/(x,y))在点藉连续。
3.有界闭域上连续函数的性质.
1)若函数/,在有界闭域DuV上连续,则./.在。
上有界,且能取得最大值与最小值;
2)若函数f在有界闭域DuV上连续,则f在。
上一致连续;
3)若函数/在有界闭域DuR,上连续,对任意的1、P*D,且/(£)
4.〃元函数唯一存在与连续可微性定理。
若1)函数%",・・・,3)在以P(«玖.."?
寸)为内点的〃+1维空间区域。
内连续;
2)偏导数氏,玲,…,F;,F;在。
内存在且连续;
AiA2A/ty
3)此,...,$>。
)=0;
4)F;0。
必莉;
则在p的某一邻域u(p)内,方程尸3,易,.."〃,力=o唯一地确定了一个定义在0x;),x;),...,x?
y°)的邻域(7(。
)上的n元连续函数y=f(x^x2,...,xn)使得:
%1(叫,易,…,尤〃,/。
],邑,…,尤〃))£U(P),3|,&,…,天)£U(Q);
F(xI,x2,...,xM,/(xpx2,...,xn))=0,(x1,x2,...,xn)GU(Q),%=fU:
),
—I
%1>=以勺如.."〃)在U(Q)内连续偏导数:
4,4—4而且九=-与,
5.由方程组确定的隐函数(隐函数组定理)
若:
1)F(x,y,u,v)与G(x,y,“,v)在以点^(x0,y0,w0,v0)为内点的区域VuR4内连续;
2)F3o,%,%Vo)=°,G3o,yo,"o,Vo)=°(为初始条件);
3)在V内EG具有一阶连续偏导数;
4)
则在点气的某一(四维空间)邻域U(£)uV内,方程组
个二元隐函数u=/(x,y),v=g(x,y),使得:
①w0=f(xQ,%),Vo=g(x0,y()),旦当(x,y)EU(0)时,
(x,y,f(x,y),g(x,y))EU(R),
F(x,y,jf(x,y),g(;r,>))三0,
GO,y,f(x,y),g(x,y))=0,
②f(x,y),g(x,y)在U(0)内连续;
③f(x,v),g(x,y)在U(0)内有一阶连续偏导数,且
1)
u(x,y),v(x,y)均是有连续的偏导数;2)-丰0.
o(x,y)
则此函数组可确定唯•的具有连续偏导数的反函数组
zx,、口3(",u)°3,)')1
工=尤(",u),,,=y(",u),且———-.—一-二1.
o(x.y)d(w.v)
(%1)多元微分学的应用
1.泰勒定理
1)若/(x,y)在点女(气,无)的邻域U(n)内存在〃+1阶连续的偏导数,则
V0)+/?
)*+#)£U(g)),有
/(^)+h,)‘O+k)=f(x°,y°)+(/?
g+AW),(x(),y())oxoy
1d73、2—、
+福(/2^_+*丁)/(尤0,乂))+…
2!
oxdy
+=("g+*g)〃/(x(),为)
n!
oxoy
iaA
+—("了+*亍尸'/3o+9/z,y°+仞:
)
(〃+1)!
dxdy
其中(晾+方""咤W*计灯
2)当吒=0,乂)=0时,相应二元函数/(x,y)的麦克劳林公式为
f(x,y)=f(。
°)+(工#+y(0,。
)+…dxdy
iaa
+-U—+y—)7(0,0)
n!
oxay
iaA
(〃+l)!
oxdy
2.极值
1)定义设函数z=/(x,y)在点气=3°,无)的某邻域U(R))内有定义,如果
V(x,y)eU(PQ)满足/(x,y)/(x0,y0)),则称f(xQ,%)为/(x,y)
的极大值(极小值),此时点丛称为f(x,y)的极大值点(极小值点)。
极大值,极小值统称极值。
2)函数/(x,y)在点藉的偏导数存在,则f在点藉取得极值的必要条件为:
f(xo,y°)=fQo,%)=°,满足上述条件的点R)称为稳定点或驻点。
3)极值的充分条件:
设函数f(x,y)在点气=(x。
%)的某邻域。
(女)内具有二阶连续的偏导数,且兄是/的稳定点。
记A=兀(鸟),眼点M),C=《(*)则
%1当B2-AC<0时,函数/•在%取得极值,若A<0,则取得极大值,若A>0,则取得极小值;
%1当B2-AC>0时,函数/在点E)不取极值;
%1当B2-AC=0时,不能判断/在点《是否极值;
3.条件极值
1)求条件极值的方法有两种:
一种将条件极值化为无条件极值的问题来求解;并一种是用拉格朗日乘数法求解。
2)拉格朗日乘数法求二元函数z=f(x,y)在约束条件(p(x,y)=0下的极值步骤如下:
%1作相应的拉格朗日函数
L(x,y,2)=f(x9y)+A(p(x,y).
%1令L=L=L,=0.即
•iya
+y)=0,
<人3,力+/1%(尤,),)=0,(p(x,y)=0.
%1求解上述方程组,得稳定点P.二(尤°,%)o
%1判定该点是否为条件极值:
如果是实际问题,可由问题本身的性质来判定,如不是实际问题,可用二阶微分判别。
3)对于条件极值的一般情形,求函数z=/(xpx2,...,x„)在约束条件
们(工|,易,...,工〃)=0,
代〃(知易,…,£)=°・
(其中f,(P\,(()2,…,Qn均具有一阶连续偏函数,且雅可比(JaCObi)矩阵
的秩为m)下的极值步骤如下:
①作拉格朗日函数
£=«/+初+部2+•••+〃广
②分别令4=Lx=...=LXn-=4=...=M=0.得到相应的方程组。
%1解上述方程组得到可能的条件极值点,再对这些点进行判定。
(%1)多元函数几何应用
1.平面曲线的切线与法线
平面曲线由方程F{xyy)=Q给出,它在点*二(气,),0)的切线与法线的方程为:
切线方程:
孩如月)3-工0)+尤(%月)3-为)=。
,
法线方程:
F'y(如y())(x-x0)-F'x(x0,y())(y-y())=0。
2.空间曲线的切线与法平面
1)空间曲线乙由参数方程==y(,),z=z(f),,E[a,/?
],表出,
假定&o),yQo),z0)不全为零,则曲线L在K=(x0,No,z°)处的切线方程式为:
尤—与二y)'o=z—z。
.
尤(撮)"())z'Qo)'
曲线L在£)=(%,)b,z°)处的法平面方程式为:
x(r0)(x-x0)+y\tQ)(y-光)+z'(r0)(z-z°)=0.
[F(x,y,z)=0
2)空间曲线乙由方程式组'给出.
[G(x,y,z)=O
业3(g,G)d(F,G)3(F,G).右,人
当:
T,「中至少一个不为零时,
3(x,y)d(z,x)3(y,z)
曲线L在点丛的切线方程为:
",G)l
3(y,z)
V_()"%)=(z-z°)3(F,G)-~3(Kg7~,3(z,x)*d(x9y)*
曲线L在点藉的法平面方程为:
3(F,G)
3(y,z)
.(、土凯凡G*(.9(F,G).(、_口
kO—尤o)+—扁3—%)+—k(z-Zo)=O。
3(2,x)3(x,y)
3.空间曲线的切平面与法线
设曲面由方程F(x,j,z)=0给出,e=(x0,y0,z0)是曲面上一点,并设函数F(x,y,z)在
偏导数在该点连续,且不同时为零,则
曲而上点K处的切平面方程为:
F;(£)3fo)+Z(*))3-yo)+E/)(z—Zo)=O,
曲面上点£)处的法线方程为:
xf()二二Z—Z。
尺(£))一兀(为一《(£)
四、基本例题解题点击
【例1】设f(x,y)是区域D:
x问极限
lim[/(x,j)+(x-l)ey]是否存在?
若存在,试求其值。
—8
y—>8
【提示】f(x9y)是k次齐次函数是指f(rx9ry)=rkf(x9y)【解】令x=rcos^,y=rsinO□同时设|/(x,y)|因limrkM=0,故limf(x,y)=lim/(rcos^,rsinff)=0.
r—>0x—8,t0'
y—>
从而lim[/(x,y)+(x-])ey]=lim(x-\)ey=-l.
XT8XT8
y—8
【例2】证明/(x,y)=7M在点(°,0)两个偏导数存在,但在点(°,°)不可微。
【证明】显然,f(0,0)=lim似,0)2(。
。
)二°,"),0)=阮些上些二0。
xtOx)—0y
因此f(x,y)=项丽在点(0,0)两个偏导数存在旦等于零.若/(x,y)=J回在点(0,0)可微,则有
f3,y)-f(0,0)=f(0,0)x+/'(0,0)y+o(7x2+/).
即f(x,y)=厢]二。
(山2+尸)((x,y)-o),但如果沿直线y=x趋于零,有
故f(x,y)=7m丰。
(JF+y2)((x,y)T0),因此/(x,y)在点(0,0)不可微。
【证明]设/=与,贝】Jg=心项)-2xn-3yf,(t)^=xn~2f\t).
疔dxdy
于是x^-+2y=ivcnf(t)-2xn~2yf(t)+2x,l~2yf\t)=nxnf(t)-nz。
oxdy
【例4】设w=/(r),其中尸=y]x2+y2+z2和f为可微分两次的函数.证明:
筋=F(r),
其中△〃=莫+宾+典,△为拉普拉斯算子.dx3)广由
【提示】计算△〃肘要计算三个二阶偏导数,而u=/(r)中x,〉,z地位是一样的,故可以考虑利用对称性,从而减少计算量。
r】Y1『2_2
【证明】—=/(r)-,r=/'(尸)=+/(〃一.由对称性即得
dxrdxrrd2uy2次r2-y2d2uz2”r2-z2
于是
」d2ud2ud2u”,,、c”/、1—、
△"=▽+▽+▽=/3)+2/(r)-=F(r).
。
)广3z~r
【例5】设x=x(y,z),y=y(x,z),z=z(x,y)为由F(x,y,z)=。
所定义的函数.证明
dxdydz——=-1.
dydzdx
Sr,志F
【证明】由H(x(y,z),y,z)=0得兀冬+兀=0,于是有:
=—T,
dydyFx
同理可得
dyF:
dzF;
dzF;'dxFz
注意的是上式一切(如%,Z。
),FOo,No,z())=o成立.因此
dxdydzFF:
Fx
dydzdxFxFyFz
【例6】设z=z(x,y)为由方程组
x=el,+v,y=eu~\z=uv
(其中”,u为参数)所定义的函数,求当w=0,v=0时也和』七.
【证明】dx=ell+v(du+dv),dy=el,~v(du-dv),dz=udv+vdu
d'z=adv2+vdu2+2dudv.
当w=0,v=0时,
dx=du+dv.dy=du一dv.dz=0,d'z=2dudv,
因此
解出血,dv得也=—(dx+dy\dv~—(cbc-dy),
d2z=2dudv=—(dx2-dy2).
【例7】求函数f=x2+y2+z2.在ox+0y+cz=l下最小值。
【解】作拉格朗日函数
L(x,y,z,X)=x2+y2+z2-X^ax+by+cz-1).
令L=L=乙;=上=0,即
2尤+人。
=0
2y+A/?
=0
2z+Ac=0
ax+by+cz=1
解得唯一驻点
cihc.-2
X=V=Z=yr=
a2+Z?
2+c2,a2+Z?
2+c2,a2+b2+c2'a2+/?
2+c2
将它们代入/•二/+y2+z2得f=-_L_70
q~+/t+cZ
因此/=x2+y2+z2.ffiax+by+cz=1卜'最小值为/nin=―=——。
a+歹+
【例8】设f(x,y)在全平面上二次可微旦恒不为零,证明f(x,y)=g(x)h(y)的充分必要条件是/(X,y)满足方程
f'fyX=fX'fy
【证明】必要性是显然的.现在证明充分性,由于/(x,y)在全平面上二次可微且恒不等于零,不妨设f(x9y)>0,令F(x9y)=Inf(x9y),则有
i一了'%一一7一
下面证明F(x,y)=In/(x,y)=p(x)+q(y),实际上由政.=。
可得F:
=p(x),因此
In/(x,y)=F(x,y)=Jp(x)dx+q(y).
这说明结论成立.■
【例9】求函数z=z(x,y)一阶和二阶的偏导数,其中x+y-^z=e~.
【证明】等式两边微分,得
dx+dy+dz=■dz①
故有dz=——(cbc+dy)=(dx-^-dy).
e"-1x+y+z-1
于是,当=g=——!
——.再将①式微分一次,得d2z=ezd2z+ezdz1.
oxoyx+y+z-l
故有d~z-——-—(也尸=一~(dx~+2dxdydy~\
e~-l/-1)
于是兰=业=兰=__=__..
3x2dxdydy2&一1](x+y+z-l)'
【例10】设可微函数z=f(x,y)对任意实数lU>0)满足f(tx,ty)=tf(x,y),点藉(1,-2,2)是曲面上一点,且人(1,-2)=4.求此曲面在点[)处的切平面方程。
【提示】/(x,y)是一次齐次函数,弄清楚齐次函数的导函数的特征很重要。
【解】由已知,对任意的点(气,为)有,/*(次0,。
'0)=〃'(工0,)'0)(*)
将(*)两边对[求导得:
工0人(■),/%)+%人(、"%)=/(如%)(**)在(**)中令r=1得:
xofx(xo,y0)+yjy(x0,y0)=/(x0,y0)
故当(%%)=(1,—2)时,(-2)x/;.(1,-2)=/(I,-2)-1xfx(1,-2)=2-4=-2.
故40-2)=i.
令F(x,y9z)=f(x,y)-z,则法线方向为〃=(/v,/v,-l).
故£)处法线方向为勺=(4,1,—1).
从而曲面在点弁处的切平面方程为4(x—l)+(y+2)—(z—2)=0.
即4x+y-z=0.
五、扩展例题解题点击
【例1】设/(x,y)在6={3,),):
尸+};2V1}上定义,若f(x,o)在点x=o处连续,而且/;(x,y)在G上有界,则/(x,y)在(0,0)处连续。
【证明】由中值定理,得
f(i,y)-f3,0)=/Q,&)(y-0)(其中00,力)
由f,(x,y)在G上有界,知BM>0,I/;(x,y)\:
.\/£>0,取々=£当Iy-01<々时有2M
(1)
l/tey)-/(-x,o)|由J'3,o)在工=0处连续,知3^>0,当|、一0|<如时,有
(2)
|/(^0)-/(0,0)|<|.
取3=min{§,③2},当|工一0|<$,|y-O|vS时,由
(1),
(2)得
I/Uy)-/(0,0)|<|/(x,y)-f(x90)|