连续型随机变量及其概率分布PPT资料.pptx

连续型随机变量及其概率分布PPT资料.pptx

《连续型随机变量及其概率分布PPT资料.pptx》由会员分享，可在线阅读，更多相关《连续型随机变量及其概率分布PPT资料.pptx（44页珍藏版）》请在冰点文库上搜索。

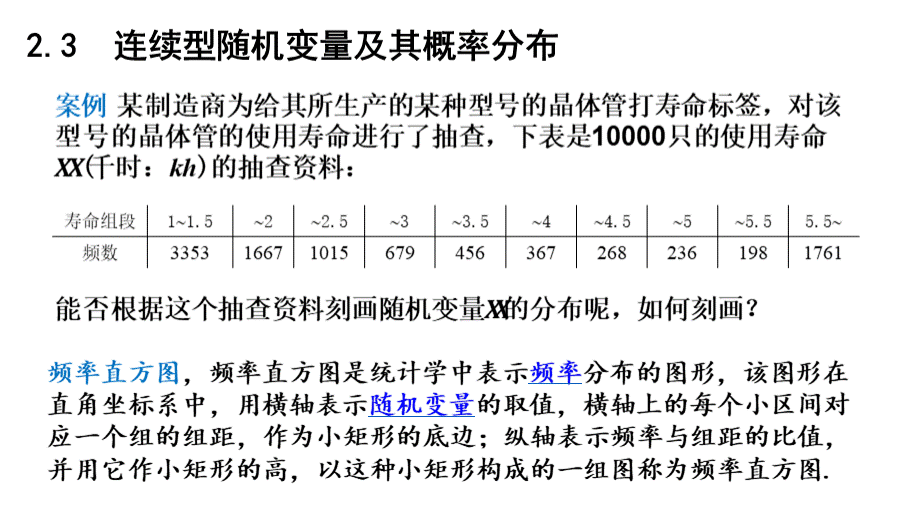
频率直方图，频率直方图是统计学中表示频率分布的图形，该图形在直角坐标系中，用横轴表示随机变量的取值，横轴上的每个小区间对应一个组的组距，作为小矩形的底边；

纵轴表示频率与组距的比值，并用它作小矩形的高，以这种小矩形构成的一组图称为频率直方图.,2.3连续型随机变量及其概率分布,2,f（x）,x,c,x10,其他,因此，从这次的抽查结果，我们认为这批晶体管的寿命的可以用这个函数、或者近似可以用这个函数刻画概率分布.,定义设X是一随机变量，F（x）是它的分布函数，若存在一个非负可积函数f（x）,使得,f（t）dtx,F（x）,x,则称X是连续型随机变量，f（x）是它的概率密度函数，简称为密度函数或概率密度.,注：

连续型随机变量的分布函数连续,-10,-5,5,0.040.02,0.06,0.08,x,f（x）,x,F（x）,分布函数F（x）与密度函数f（x）的几何意义,yf（x）,概率密度函数f（x）的性质,1、,f（x）0,2、f（x）dxF（）1常利用这两个性质检验一个函数能否作为连续性随机变量的密度函数，或求其中的未知参数,3、在f（x）的连续点处，,f（x）F（x）,f（x）描述了X在x附近单位长度的区间内取值的概率f（x0）xP（x0Xx0x）,注：

对于连续型随机变量X,P（X=a）=0（这里a可以是随机变量X的一个可能的取值）,xXa）,a）P（a,0P（X0P（X,a,ax,x0f（x）dx,a）lim,x0,a,ax,f（x）dx,0,P（Xa）0命题连续型随机变量取任一常数的概率为零强调概率为0

（1）的事件未必不发生（发生）,（Xa）（axXa）,事实上,对于连续型随机变量XP（aXb）P（aXb）P（aXb）P（aXb）,b,a,f（x）dxF（b）F（a）,b,x,f（x）,-10,-5,5,0.060.040.02,0.08,a,P（Xb）P（Xb）F（b）,x,P（Xa）P（Xa）1F（a）f（x）,-10,-5,5,0.080.060.040.02,a,例设随机变量X具有概率密度函数,x0;

0,x0.,f（x）,Ae3x,试确定常数A，以及X的分布函数.,解由1,A,13,f（x）dx,0,Aedx,3x,x0;

0,x0.,3e3x,知A=3，即f（x）而X的分布函数为,1e3x,x0;

x0.,f（t）dt,F（x）,x,0,例有一批晶体管，已知每只的使用寿命X为连续型随机变量，其概率密度函数为,2,c,x1000,f（x）,0,其他,x,

（1）求常数c.,（c为常数）,已知一只收音机上装有3只这样的晶体管，每只晶体管能否正常工作相互独立，求在使用的最初1500小时三只晶体管中损坏的只数所服从的分布.这样的晶体管,使用的最初1500小时只有一个损坏的概率.,解

（1）,令dx1,c,x2,f（x）dx,1000,c=1000,

（2）,设事件A表示一只晶体管的寿命小于1500小时P（A）P（0X1500）,1500,x2,1000,1000dx1,3,设在使用的最初1500小时三只晶体管中,损坏的只数为,1,YB3,3,（3）,49,122,P（Y1）C1,333,例一个靶子是半径为2米的圆盘，设击中靶上任一同心圆盘上的点的概率与该圆盘的面积成正比，并设射击都能中靶，以X表示弹着点与圆心的距离，试求随机变量X的分布函数,解:

若x0,则（Xx）是不可能事件,于是,F（x）P（Xx）0若0x2,由题意,P（0Xx）kx2,k是某一常数.,4,x2,即P（0Xx）,于是,F（x）P（Xx）,4,P（X0）P（0Xx）,x2,4,取x2,有P（0X2）k221,k1,F（x）P（Xx）1综上所述，随机变量X的分布函数为,1,0x2,F（x）4,x00x2x2,若x2,由题意,是必然事件,于是,

（1）均匀分布,常见的连续性随机变量的分布,XU（a,b）,记作,X的分布函数为,0,ba,xa,F（x）,1,xb,axb,xa,1,f（x）ba,0,axb,其他,若X的密度函数为,则称X服从区间（a,b）上的均匀分布,x,f（x）,a,b,x,F（x）,b,a,1,ba,。

。

1,（c,d）（a,b）,1dxdc,cba,P（cXd）d,ba,即X的取值在（a,b）内任何长为dc的小区间的概率与小区间的位置无关,只与其长度成正比.这正是几何概型的情形.,

（2）指数分布若X的密度函数为,ex,x0f（x）0,其他,则称X服从参数为的指数分布,XExp（）,记作,X的分布函数为,0,x,F（x）,x01e,x0,0为常数,x,F（x）1,0,x,0,f（x）,相继两次故障时间间隔T的概率分布；

设备已经无故障运行8小时的情况下，再无故障运行10小时的概率.,例假定一大型设备在任何长为t的时间内发生故障的次数X（t）服从参数为t的泊松分布.求：

解

（1）,FT（t）P（Tt）,0,t01P（Tt）,t0,P（T,0!

（t）0et,t）P（N（t）0）0,t0,t0,t,F（t）,1e,t,f（t）,et0,t0e,t0,即,TE（）,P（T8）,

（2）P（T18T8）P（T18）1F（18）e10,1F（8）,指数分布具有无记忆性：

P（Xst|Xs）P（Xt）,XExp（）,则,例（常识）（0,t）内的保险公司索赔次数N（t）服从poisson分布即N（t）P（t）；

其两次索赔之间的时间间隔服从指数分布。

例（常识）（0,t）内某柜台需要服务的顾客数N（t）服从poisson分布即N（t）P（t）；

先后两个顾客到达柜台的时间间隔服从指数分布。

例某美容厅顾客到达后需要等候的服务时间服从参数为0.1的指数分布，若顾客等候时间超过,20分钟就会离开.

（1）请给出该美容厅在营业时间内50个顾客中因等候时间超过20分钟，没有等到服务而离开人数的分布律;

（2）50个顾客中没有等到服务而离开的人数大于1的概率.,X,10,P（X20）,0.1e,0.1x,2,dxe,50,kk250k,P（Yk）Cp（1e）,，k0,1,2,50,X,解设Y表示50个顾客中因等候时间超过20分钟，没有等到服务而离开的人数，根据题意每个顾客等待时间,超过20分钟的概率为,的50重Bernoulli试验中顾客,Y可以看成是pe2离开发生次数，因此YB（50,e2）,

（2）没有等到服务而离开的次数大于1的概率为,P（Y1）1p（Y0）p（Y1）1（1e2）5050e2（1e2）49,（3）正态分布（Gauss分布）若X的密度函数为,x,f（x）,e,（x）2,22,12,则称X服从参数为m,s,2,的正态分布,记作XN（m,s2）,为常数，0,N（-3,1.2）,0.30.250.20.150.10.05-6-5-4-3-2-1,3,f（x）的性质：

图形关于直线x=对称：

f（+x）=f（-x）在x=时,f（x）取得最大值12在x=时,曲线y=f（x）在对应的点处有拐点曲线y=f（x）以x轴为渐近线曲线y=f（x）的图形呈单峰状,12,P（X）F（）1F（）P（X）,-6,-5,-4,-3,-2,-1,0.30.250.20.150.10.05,f（x）的两个参数：

位置参数即固定,对于不同的,对应的f（x）的形状不变化，只是位置不同形状参数固定，对于不同的，f（x）的形状不同.,若12则,112122,比x=2所对应的拐点更靠近直线x=,附近值的概率更大.,x=1所对应的拐点,前者取,Showfn1,fn3,大,小,0.20.1,0.3,0.4,0.5,几何意义,数据意义,-6-5-4-3-2-1大小与曲线陡峭程度成反比大小与数据分散程度成正比,x其分布函数为,x2,一种重要的正态分布：

N（0,1）标准正态分布标准正态分布的计算：

如果随机变量XN0，1，则其密度函数为,2,1,2,e,x,1,2,x,xtdt,x,t2,e2dt,教科书上都附有标准正态分布表,由此可得（x）值.（0）0.5（x）1（x）P（|X|a）2（a）1,-3-2-1,1,2,3,0.40.30.20.1,（0）0.5,2,3,0.40.30.20.1,-3-2-x-1,1x,（x）1（x）,P（|X|a）2（a）1,对一般的正态分布：

XN（,2）,其分布函数F（x）,x,edt,12,22,（t）2,t作变量代换s,F（x）x,P（aXb）F（b）F（a）,ba,P（Xa）1F（a）,1a,定理若XN（,2）,则,XN（0,1）.,例假定某人群血液中总胆固醇含量（.,.）（/），如果总胆固醇超过5.6被认为是偏高的，求总胆固醇偏高的概率.,P（X5.6）1P（X5.6）,0.8,15.64.2,1（1.75）=10.95994=0.04006,解,例假设公共汽车车门的高度是按男子与车门顶碰头机会在1%以下来设计的，假设成年男子身高（,）（），问如何设计车门的高度？

解设车门的高度为（），按设计要求解满足（）.,查表得.=.，所以取,=.，,解得,或（）.的最小值.,=.,例已知XN（2,2）且P（2X4）=0.3,求P（X0）.,解一,P（X0）0212,P（2X4）4222,2（0）0.3,20.8,P（X0）0.2,-2,2,4,6,0.05,0.150.1,0.2,解二图解法,0.2,由图P（X0）0.2,0.3,例3原则,设XN（,2）,求,P（|X|3）,解P（|X|3）P（3X3）,33,3323120.998710.9974一次试验中,X落入区间（-3,+3）的概率为0.9974,而超出此区间可能性很小由3原则知，当a3时（a）0,b3时（b）1,例设测量的误差XN（7.5,100）（单位：

米）,问要进行多少次独立测量，才能使至少有一次误差的绝对值不超过10米的概率大于0.9?

解,1010,P（|X|10）107.5107.5,0.251.750.2511.750.5586设A表示进行n次独立测量至少有一次误差的绝对值不超过10米,P（A）1（10.5586）n0.9,n3,所以至少要进行4次独立测量才能满足要求.,